| | Адрес этой страницы (вложенность) в справочнике dpva.ru: главная страница / / Техническая информация / / Физический справочник / / Звук. Ультразвук / / Частоты нот. Частота звуковой волны для нот всех октав. + Настройка струн шестиструнной гитары — частота звука. «Разгерцовка нот». Поделиться:
 Введите свой запрос: Введите свой запрос: | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Если Вы не обнаружили себя в списке поставщиков, заметили ошибку, или у Вас есть дополнительные численные данные для коллег по теме, сообщите , пожалуйста. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Коды баннеров проекта DPVA.ru Начинка: KJR Publisiers Консультации и техническая | Проект является некоммерческим. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Владельцы сайта www.dpva.ru не несут никакой ответственности за риски, связанные с использованием информации, полученной с этого интернет-ресурса. Free xml sitemap generator | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Частоты различных нот
Частоты различных нот
Частоты колебаний соседних ступеней хроматической гаммы отличаются
на 5,94630943593.![]() ..% или в
=1,0594630943593…
раз. Путем деления любой известной нам частоты на этот коэффициент
мы получаем нисходящие частоты соседних полутонов, а путем
умножения — восходящие.
Имея под рукой калькулятор, не трудно вычислить, например, частоту
ноты ЛЯ# 1-й октавы, зная частоту
соседней ноты ЛЯ 1-й октавы (440 Гц):
440*1,05946…= 466,1637615…Гц.
..% или в
=1,0594630943593…
раз. Путем деления любой известной нам частоты на этот коэффициент
мы получаем нисходящие частоты соседних полутонов, а путем
умножения — восходящие.
Имея под рукой калькулятор, не трудно вычислить, например, частоту
ноты ЛЯ# 1-й октавы, зная частоту
соседней ноты ЛЯ 1-й октавы (440 Гц):
440*1,05946…= 466,1637615…Гц.
Ниже в таблице приведены частоты нот хроматической гаммы от контроктавы до второй октавы, округленные до одного знака после запятой.
| Нота | 25511382573973″ x:fmla=»=B20/POWER(2,1/12)» bordercolorlight=»#FFFFFF» bordercolordark=»#FFFFFF»> Частота (Гц) | |
| 2-я |
e |
659,3 (1-я струна скрипки, мандолины, 4-струнной домры) |
|
d# |
25396744416162″ x:fmla=»=B21/POWER(2,1/12)» bordercolor=»#FFFFFF» bordercolorlight=»#FFFFFF» bordercolordark=»#FFFFFF»> | |
d |
587,3 |
|
|
c# |
554,4 |
|
|
c |
25113060119702″ x:fmla=»=B24/POWER(2,1/12)» bordercolor=»#FFFFFF» bordercolorlight=»#FFFFFF» bordercolordark=»#FFFFFF»> | |
|
1-я
|
h |
493,9 |
|
b |
16376151808964″ x:fmla=»=B26/POWER(2,1/12)» bordercolor=»#FFFFFF» bordercolorlight=»#FFFFFF» bordercolordark=»#FFFFFF»> | |
|
a |
440,0 |
|
|
g# |
415,3 |
|
|
g |
99543598174898″ x:fmla=»=B29/POWER(2,1/12)» bordercolor=»#FFFFFF» bordercolorlight=»#FFFFFF» bordercolordark=»#FFFFFF»> | |
|
f# |
370,0 |
|
|
f |
349,2 |
|
|
е |
62755691286964″ x:fmla=»=B32/POWER(2,1/12)» bordercolor=»#FFFFFF» bordercolorlight=»#FFFFFF» bordercolordark=»#FFFFFF»> | |
|
d# |
311,1 |
|
|
d |
293,7 |
|
|
c# |
18263097687185″ x:fmla=»=B35/POWER(2,1/12)» bordercolor=»#FFFFFF» bordercolorlight=»#FFFFFF» bordercolordark=»#FFFFFF»> | |
|
c |
261,6 |
|
|
Малая
|
h |
94165062806181″ x:fmla=»=B37/POWER(2,1/12)» bordercolor=»#FFFFFF» bordercolorlight=»#FFFFFF» bordercolordark=»#FFFFFF»> |
|
b |
233,1 |
|
|
a |
220,0 |
|
|
g# |
65234878997231″ x:fmla=»=B40/POWER(2,1/12)» bordercolor=»#FFFFFF» bordercolorlight=»#FFFFFF» bordercolordark=»#FFFFFF»> | |
|
g |
196,0 |
|
|
f# |
185,0 |
|
|
f |
61411571650169″ x:fmla=»=B43/POWER(2,1/12)» bordercolor=»#FFFFFF» bordercolorlight=»#FFFFFF» bordercolordark=»#FFFFFF»> | |
|
е |
164,8 |
|
|
d# |
155,6 |
|
|
d |
83238395870353″ x:fmla=»=B46/POWER(2,1/12)» bordercolor=»#FFFFFF» bordercolorlight=»#FFFFFF» bordercolordark=»#FFFFFF»> | |
|
c# |
138,6 |
|
|
c |
130,8 |
|
|
Большая
|
h |
123,5 |
|
b |
116,5 |
|
|
a |
110,0 |
|
|
g# |
103,8 |
|
|
g |
98,0 |
|
|
f# |
92,5 |
|
|
f |
87,3 |
|
|
е |
82,4 |
|
|
d# |
77,8 |
|
|
d |
73,4 |
|
|
c# |
69,3 |
|
|
c |
65,4 |
|
|
Контр
|
h |
61,7 |
|---|---|---|
|
b |
58,3 |
|
|
a |
55,0 |
|
|
g# |
51,9 |
|
|
g |
49,0 |
|
|
f# |
46,2 |
|
|
f |
43,7 |
|
|
е |
41,2 (нижняя струна контрабаса, 4-струнной басгитары, балалайки-контрабас) |
Как видно из таблицы, через октаву любая частота удваивается, благодаря той самой двойке, корень 12-й степени из которой (по количеству полутонов в хроматической гамме) мы и извлекали.
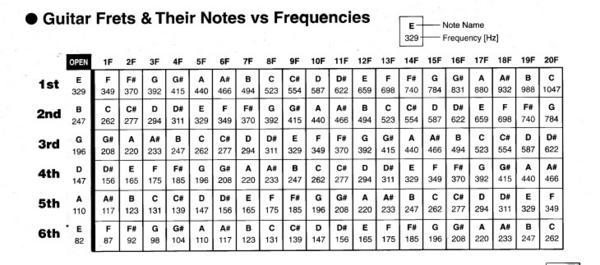
Частоты настройки открытых струн наиболее распространенных струнных инструментов:
| Смычковые | ||||
|
Скрипка |
Альт | Виолончель | Контрабас | |
|
1) ми — 659,3 Гц 2) ля — 440 Гц 3) ре — 293,7 Гц 4) соль — 196 Гц |
1) ля — 440 Гц 2) ре — 293,7 Гц 3) соль — 196 Гц 4) до — 130 Гц |
1) ля — 220 Гц 2) ре — 146,8 Гц 3) соль — 98 Гц 4) до — 65 Гц |
1) соль — 98 Гц 2) ре — 73,4 Гц 3) ля — 55 Гц 4) ми — 41,2 Гц |
|
| ГИТАРЫ | ||||
|
6 -струнная |
«Русская» 7 -струнная | «Американская» 7 -струнная | Бас-гитара | |
|
1) ми — 329,6 Гц 2) си — 246,9 Гц 3) соль — 196 Гц 4) ре — 146,8 Гц 5) ля — 110 Гц 6) ми — 82,4 Гц |
1) ре — 293,7 Гц 2) си — 246,9 Гц 3) соль — 196 Гц 4) ре — 146,8 Гц 5) си — 123,5 Гц 6) соль — 98 Гц 7) ре — 73,4 Гц |
1) ми — 329,6 Гц 2) си — 246,9 Гц 3) соль — 196 Гц 4) ре — 146,8 Гц 5) ля — 110 Гц 6) ми — 82,4 Гц 7) си — 61,7 Гц
|
1) соль — 98 Гц 2) ре — 73,4 Гц 3) ля — 55 Гц 4) ми — 41,2 Гц |
|
| БАЛАЛАЙКИ | ||||
| Прима | Секунда | Альт | Бас | Контрабас |
|
1) ля — 440 Гц 2-3) ми — 329,6 Гц |
1) ре — 293,7 Гц 2-3) ля — 220 Гц |
1) ля — 220 Гц 2-3) ми — 164,8 Гц |
1) ре — 146,8 Гц 2) ля — 110 Гц 3) ми — 82,4 Гц |
1) ре — 73,4 Гц 2) ля — 55 Гц 3) ми — 42,1 Гц |
| ДОМРЫ | ||||
| Малая | Альт | Бас |
Прима 4-струнная |
Мандолина |
|
1) ре — 587,3 Гц 2) ля — 440 Гц 3) ми — 329,6 Гц
|
1) ре — 293,7 Гц 2) ля — 220 Гц 3) ми — 164,8 Гц
|
1) ре — 146,8 Гц 2) ля — 110 Гц 3) ми — 82,4 Гц |
1) ми — 659,3 Гц 2) ля — 440 Гц 3) ре — 293,7 Гц 4) соль — 196 Гц |
1) ми — 659,3 Гц 2) ля — 440 Гц 3) ре — 293,7 Гц 4) соль — 196 Гц |
Кто может объяснить теорию музыки языком программирования? — Хабр Q&A
Ниже идет мое понимание теории музыки, которое не претендует на точность и полноту.Звук — это колебания воздуха с определенной амплитудой и частотой. Амплитуда отвечает за громкость звука. Частота отвечает за высоту (тон) звука, грубо говоря за его восприятие, окраску.
Если мы возьмем любой реальный звук (например, колебания струны), то в его спектре будет не только одна главная частота, а будет набор частот (гармоник), которые называются обертонами. Главная гармоника называется основной тон, и дальше идут 1-я гармоника,2-я и т.д. Обычно частоты обертонов относятся к частоте основного тона как правильные дроби. Так первая гармоника по частоте в два раза больше, чем основной тон, вторая гармоника относится как 3/2 и т.д.
Из этого следует очень интересный факт. Звук высотой x звучит для человека практически одинаково со звуком высотой 2*x потому, что для звука высотой x 1-я гармоника будет как раз высотой 2*x , т.е. их спектры будут практически одинаковы. А раз так, то мы можем сделать один интересный трюк.
Зафиксируем частоту x. 1-я гармоника будет высотой 2*x . Получим интервал [x; 2*x]. Этот интервал называется октавой. Возьмем 2-ю гармонику, она будет относится к основной частоте как 3/2 * x. Если полученная высота выходит за пределы интервала нашей октавы [x; 2*x], то сделаем следующий трюк. Будет считать что полученная высота на самом деле является 1-й гармоникой какого-то другого звука, который лежит внутри нашего интервала [x; 2*x]. Таким образом мы получаем новый какой-то тон внутри нашей октавы. Далее берем 3-ю гармонику высоты x и также спускаем его в нашу октаву [x; 2*x].
В результате этого процесса внутри октавы [x; 2*x] можно построить 7 тонов, которые (что удивительно) составляют некоторую систему (с точки зрения восприятия человеком). Т.е. эти все 7 тонов обладают внутренними тяготениями, связями, которые можно как-то использовать. Так вот эти все 7 тонов называются натуральным ладом, а связи внутри лада называются ладовыми тяготениями.
При этом внутри лада есть два измерения. Ноты внутри лада можно играть последовательно, одну за другой. Это называется мелодия. Но ноты внутри лада можно же играть одновременно. При этом оказалась, что если играть одновременно три ноты, построенные через одну ступень, то получится система трезвучий (аккордов), которая в свою очередь также обладает собственными закономерностями, там всякие тонический, субдоменантовый и доминантные аккорды и т.д. Плюс если мы сюда добавим ритм, то и получим все главные соствляющие музыки: мелодия, ритм, гармония.
В реальности натуральные лады можно строить немного разными способами, получая каждый раз немного разные устойчивые системы. Натуральные ладов много. Самыми древними являются всякие разные пентатоники — устойчивые системы из пяти, а не семи нот и т.д.
Когда в средние века музыка стала широким общественным явлением, остро возник вопрос о стандартизации. Каждый музыкант может использовать собственный натуральный ряд, что означает, что вместе с другим музыкантом сыграть уже не получится.
Вопрос о стандартизации решили следующим образом. Выбрали одну базовую частоту, пусть это будет Ля — 440 Гц. После этого весь диапазон звуков разбили на октавы, уменьшая и увеличивая базовую частоту в два раза. А каждую октавую разбили на 12 равных частей — нот. При таком разбиении оказалось, что от каждой из 12 нот можно построить мажорный и минорный лады из 7 нот. Мажорный лад строится по системе : тон-тон-полутон… и т.п. (могу ошибаться), минорный: тон-полутон-тон и т.п. (могу ошибаться). Мажорный и минорные лады являются неплохими приближениями натуральных ладов, хотя звучат и не так идеально. Но к этому за многие годы уже все привыкли, стандарты оказались главнее, а человек приспособился.
Таким образом мы имеем в октаве 12 нот и два лада: мажор и минор. Таким образом получаем 24 звукосистемы из 7 нот. Такая система и называется тональностью. Например, до-мажор, си-бемоль-минор и т.п. Каждая тональность обаладет своей эмоциональной окраской.
Как доказательство концепции, Бах написал набор пьес «Хорошо темперированный клавир», где использовал все тональности.
Собственно теория музыки и изучает все закономерности ладов и нарабатывает более-менее стандартные схемы использования.
бредогенерация с частотой 432 Гц / Блог компании Pult.ru / Хабр
“Чем чудовищнее ложь, тем охотнее толпа в неё верит!”П.Й. Геббельс
Как и у большинства моих постов — у этого есть причина. Сравнительно недавно один из моих случайных собеседников решил впечатлить меня знанием истории музыки и поведал много “интересного” о эталоне настройки ноты “ля” первой октавы. К слову, по первому впечатлению человеком он был неглупым (пока не начал рассказывать про частоту 432 Гц) и, по его словам, являлся выпускником Санкт-Петербургской государственной консерватории им. Римского-Корсакова. Рассказ собеседника изобиловал массой псевдоисторических “отступлений” и апелляцией к исследованиям математика Фибоначчи и наследию Джузеппе Верди.
С верующими спорить бессмысленно, поэтому я решил узнать о частотном мифе побольше у гугла и столкнулся чудовищной картиной. Оказалось, что рунет изобилует антинаучными и эзотерическими рассуждениями относительно эталонных частот для музыкального строя. Количество желтого конспирологического контента просто поражает. Разумных и адекватных публикаций на эту тему сравнительно немного, а их посещаемость значительно ниже чем у откровенной чуши.
Уровень аргументации большинства оккультно-мракобесных источников едва ли может впечатлить мало-мальски грамотного школьника. Несмотря на это я решил добавить ещё одну ложку правдивого дегтя в море приторно сладкой и ядовитой для здравого смысла эзотерической медовухи.
В принципе, абсурдность утверждений моего собеседника вряд ли требует подробного анализа и доказательства — бред очевиден. Миф основательно развенчан, но для тех, кто случайно повёлся и не утратил при этом трезвость мысли я приведу несколько наиболее веских аргументов под катом. Мне интереснее другое, по какой причине такого рода чушь приобретает популярность, чему будет посвящен отдельный раздел сего опуса.
Геббельс и Рокфеллер украли “правильную” ноту “ля”
Сторонники теории “музыкального заговора” буквально убеждены в том, что существующий сегодня эталонный стандарт для настройки ноты “ля” первой октавы (440 Гц) — “неправильный”, “вредный” и способствует “превращению людей в больных рабов”. При этом утверждается, что нота “ля” 432 Гц и музыкальный строй, созданный на её основе, воспринимается человеком лучше, так как эта частота “соответствует биоритмам”, “резонирует с водой”, “связана с числами Фибоначчи”, “гармонирует с ритмами вселенной”, “исцеляет от страшных недугов” и просто поднимает настроение.
Господа конспирологи также утверждают, что частота 432 Гц для ноты “ля” применялась с незапамятных античных времен, в частности, была ходовой для древних Греции и Египта. Позже её якобы очень ценили Вольфганг Амадей Моцарт и Джузеппе Верди. Именем последнего эта частота названа сегодня.
Самое интересное то, как описывают смену этой частоты. Тут мнения конспирологов расходятся. Одни утверждают, что “наезд” на “истинную “ частоту начался ещё в 19-м веке и обвиняют Гельмгольца (по всей видимости потому, что тот действительно много думал о стандартизации музыкального строя, и, вероятно, создал-таки камертон с “демонической” частотой 440 Гц).
Другие грешат на Рокфеллеров, заявляя, что без изменения музыкального строя эти видные финансисты не смогли бы получить тотальный контроль над человечеством и фондовыми рынками. Третьи традиционно спихивают все на национал-социалистическую рабочую партию Германии, утверждая, что именно геноссе Геббельс обладал тайным знанием о “не правоверности” частоты 440 и ее пагубном влиянии на людей.
Преследуя тайную цель порабощения народов, нацисты внедрили в практику новый музыкальный строй на всей территории Рейха, а применение частоты 432 Гц для ноты “ля” 1-й октавы запретили под страхом мучительной смерти в безэховой газовой камере концлагеря Заксенхаузен. Иными словами, всё самое ужасное в мире связано с демоническим звуком ноты “ля” на частоте 440 Гц и музыкальном строе, созданном на её основе.
Пару слов о том, как всё обстоит на самом деле
Начну, пожалуй, с античных инструментов. По заявлению таких видных историков как Sifakis G. Μ. (“The Function and Significance of Music in Tragedy”, London, 2001.) и Скржинской М.В. (“Древнегреческие праздники в Элладе и Северном Причерноморье / — СПб. 2010), античные музыкальные инструменты археологи находят в небольшом количестве и подавляющем большинстве в виде фрагментов. Камертоны для настройки античных музыкальных инструментов не использовались, строили на слух, ориентируясь на собственный голос.
Далее про Верди и Моцарта. Моцарт использовал камертон, созданный Йоханом Андреасу Штайном, известным венским настройщиком. Измерения показали, что камертон Штайна настроен на частоту 421,6 Гц. Кроме того, услугами Штайна пользовались Гайдн, Сальери и Бетховен. Это может свидетельствовать о том, что они также использовали частоту 421,6 Гц для ноты “ля” первой октавы. Сравнительно недавно был обнаружен камертон Генделя для настройки рояля. Измерения показали, что “ля” Генделя было немного выше чем у Моцарта, частота составляла 422,5 Гц.
На протяжении 18-го и почти всего 19-го столетия не существовало никакой эталонной частоты. Для разных залов, оперных театров и церквей (в случаях с органами) диапазон частот для ноты “ля” варьировался в пределах от 400 до 460 Гц. Впервые общепризнанный стандарт для ноты “ля” первой октавы был введен в Европе в 1859-м году, идею о стандартизации предложили концертные площадки Франции. В соответствии с этим стандартом нота “ля” настраивалась на 435 Гц.
Верди единственный композитор, который упомянул строй и частоту 432 Гц в 1900-м году, так как сначала завещал потомкам исполнять его реквием с «ля» частотой 435 Гц в соответствии с французским стандартом 1859 года, а позже сделал упоминание о том, что имеет смысл снизить частоту на 3 Гц (т.е. до 432-х). Причиной были не духовные особенности частоты и не ее якобы эстетическая ценность, а желание композитора сохранить аутентичность произведения и его поддержка единого французского стандарта.
К слову, о самих измерениях и Герцах, как единицах. Возможность сравнительно точно измерить частоту появилось в 1834 году, благодаря таким приборам как зубчатое колесо Савара и тонометра Шейблера. В качестве единицы измерения частоты были выбраны циклы в секунду, которым в 1930-м году было присвоено имя великого Герца.
Первое международное соглашение о принятии в качестве стандарта для ноты “ля” первой октавы частоты 440 Гц было принято на конференции в Британском институте стандартов в Лондоне в 1939 году. Немецкая делегация и тем более Геббельс при всём желании не могли участвовать в этой конференции, в связи с началом Второй мировой войны. В Германии этот стандарт был принят только в 1955-м году вместе со стандартом ISO 16.
Также рекомендую к просмотру и прочтению следующие материалы на эту тему:
Раз и два.
Неиссякаемый фонтан человеческой глупости
Говоря совсем откровенно, мне было сложно поверить, что такое внушительное количество людей в России легко покупается на глупость о “всеблагой” ноте “ля”. Уверен, что предыдущий раздел в этом посте не открыл Америки для подавляющего большинства читателей. Интересно другое, каким образом вполне адекватных людей, знакомых со школьным курсом физики, а также с основами музыкальной теории, убеждают в откровенной ахинее? Почему многие люди, часто молодые, склонны верить этому и другим мифам?..
Механизм убеждения достаточно прост. К бредовым умозаключениям примешивают мнение авторитетов, как в данном случае произошло с Джузеппе Верди. Крошечную фразу Верди (вырванную из контекста) про “ля” такой-то частоты, “великие гуру современности” превращают в доказательство своих маргинальных взглядов на стандарт. Первоисточник вряд ли доступен в сети и проверить будет достаточно сложно.
Далее, для пущей убедительности выдумывается история про античные инструменты, о которых даже археологи знают сравнительно немного (многие существуют только в качестве продуктов исторического моделирования, созданных на базе откопанных запчастей и изображений на амфорах). И тут же к “всеблагой” частоте примазывают имена античных мыслителей, сделавших первые шаги в теории музыки, в данном случае Пифагора. Исторический базис уже есть, становится ещё правдоподобнее.
Следующий шаг убеждающего мифотворчества — создание мировоззренческого конфликта. Цель конфликта — противопоставить продвигаемую ахинею чему-то страшному и демоническому, например Геббельсу или Рокфеллеру (тут в зависимости от целевой аудитории). Это автоматически превратит альтернативные точки зрения, во вражескую пропаганду, а, соответственно, в нечто недостойное внимания истинного адепта “частоты света и добра”.
Для создания иллюзии научности всего изложенного числовое значение частоты, путем нумерологической спекуляции подгоняется под что-нибудь, связанное с человеческой физиологией, теоретической физикой, математикой или астрономией (биотоки мозга, частота сердечных сокращений, частота земли, солнца, воды, резонанс Шумана, числа Фибоначчи, ряды Фурье и т.п.). Обилие числовых значений в этих науках даёт туфтологам богатый выбор. Достаточно даже не прямых, а косвенных совпадений, например, частота одного из колебаний резонанса Шумана около 8 Гц (7,83 Гц), если умножить 8 на “правильную” цифру 54, то получится 432, а если на “неправильную” 55 — 440.
Реальные частоты даже косвенно не связаны с числом 432, конспиролухи обычно подгоняют даже сами числовые значенияДля особо впечатлительных людей с визуальным типом восприятия записываются “эксперименты” с песком или мукой, наподобие представленного ниже:
На самом деле фокус доказывает лишь то, что материал резонирует на на нужной “исследователю” частоте. При этом заявляется, что правильные геометрические формы — суть неизученные наукой явления связанные с “божественной частотой”.
О причинах, по которым технология внедрения мифа в массовое сознание хорошо работает, можно писать книгу. Я усматриваю несколько причин, которые особенно хорошо подходят для России. Снижение уровня школьного и прочего образования, на фоне массовой потери интереса к обучению. Практически всё для того, чтобы распознать чушь, есть в школьной программе, но у учащихся нет мотивации к запоминанию, а у преподавателей инструментов для развития мотивации.
Коммерческая раскрутка оккультных и эзотерических верований через СМИ, обилие контента в сети. Сюда легко отнести многочисленные “реалити”-шоу и даже целые телеканалы в кабельном вещании, которые пропагандируют псевдонауку и эзотерическое мракобесие. Деньги не пахнут, и ради рейтингов на благодатную почву атавизмов русского языческого мировосприятия падают зерна “тайных оккультных парадигм”. Аналогичная ситуация эхом развивается в рунете, где каждый 10-й видеоблоггер скоро станет “просветленным”, “всевидящим”, “святым”, достигшим нирваны через постижение таинств “великой и всеблагой” частоты 432 Гц.
Недоверие к науке и сомнение в научных авторитетах. Сложность современных научных открытий и разработок, неспособность их понять без достаточного уровня знаний, вызывают массовое недоверие к науке, снижая авторитет ученых в глазах широкой общественности. В поисках доступных и понятных мировоззренческих ориентиров, многие люди начинают смотреть на реальность через розовые оккультно-эзотерические призмы.
Итог
Предлагаю читателям самим подвести статистическую черту под моими рассуждениями и принять участие в опросе, который размещен ниже.
Немного корпоративной джинсы.
В нашем каталоге есть музыкальные инструменты и аппаратура для создания музыки. Почти все инструменты можно настраивать, используя в качестве эталона любую из понравившихся вам частот, в том числе 421,6 Гц, 422,5 Гц, 435 Гц, и, конечно, святые 432 Гц и зловещий стандарт 440 Гц.
Кроме того напоминаю, что с 10 по 12 ноября в Москве пройдет Moscow Hi-End Show — выставка традиционно представляющая лучшее из того, что есть на аудиорынке: современные АС,
портативную аудиоэлектронику, проигрыватели винила, домашние решения для AV и др.
Гостей столицы ждут комфортные номера отеля Holiday Inn Tagansky.
В шоу принимают участие производители и дистрибьюторы High End Audio из России и зарубежных стран, будет работать винил-бутик, пройдут семинары для пользователей и живые концерты.
Вход на выставку бесплатный.
График работы:
10 ноября: с 12 до 20 часов
11 ноября: с 11 до 19 часов
12 ноября: с 11 до 17 часов
Получить пригласительный билет
Подробнее о выставке
В материале использован фотоконтент ask.audio
Математика музыкального строя — основы.: rainy_sunny — LiveJournal
Сегодня я расскажу о том, что такое чистые музыкальные интервалы, почему невозможна абсолютная их чистота и на какие компромиссы музыкантам приходилось идти из-за этого. [Cпойлер]И до сих пор приходится! Кто верит во вселенскую гармонию, лучше не читайте, тлен гарантирован )Для понимания потребуется базовое знакомство с нотами и интервалами. В поcте много цифр, но вам считать ничего не придётся, достаточно понимать, что происходит.
Любую музыкальную ноту можно выразить цифрой — частотой колебания в герцах. А интервал между двумя нотами — соотношением двух частот. Например, нота на октаву выше данной всегда имеет частоту в 2 раза больше. Поэтому октава — это соотношение 2:1 или множитель 2.
Когда я буду говорить «интервал между двумя нотами равен 5:4», я буду иметь в виду, что частота более высокой ноты в 5:4 (или 1,25) раз выше, чем частота нижней ноты.
Имеет значение именно соотношение («во сколько раз выше»), а не разница частот («на сколько герц больше»). Например, между 100 и 200 Гц такой же интервал, как между 300 и 600 Гц, — октава (2:1).
Чтобы сложить два интервала, мы перемножаем их соотношения. «На октаву выше» значит «в 2 раза выше по частоте», поэтому на две октавы выше — в 4 раза выше, на три октавы — в 8 раз выше, и так далее.
—
Интервалы, которые выражаются простым соотношением (то есть дробью, у которой и числитель и знаменатель — небольшие целые числа), называются чистыми интервалами.
Основные чистые интервалы:
2:1 — октава
3:2 — квинта
4:3 — кварта
5:4 — большая терция
6:5 — малая терция.
Если интервал между нотами чистый, то эти ноты очень хорошо «сливаются» вместе. Музыканты издавна стремились к таким созвучиям.
Этому есть физическое объяснение. Любая нота состоит из гармоник — колебаний, кратных друг другу по частоте. Если соотношение между нотами простое, то часть гармоник у этих двух нот будут совпадать и полностью сливаться друг с другом.Например, возьмём ноту с частотой 300 Гц и ноту на октаву выше (300*2=600 Гц) и выделим у них общие гармоники:
300, 600, 900, 1200, 1500, 1800, 2100, 2400,…
600, 1200, 1800, 2400,…Теперь возьмём ноту с частотой 300 Гц и ноту на чистую квинту выше:
300, 600, 900, 1200, 1500, 1800, 2100, 2400, 2700,…
450, 900, 1350, 1800, 2250, 2700,…На спектрограмме эти совпадающие гармоники хорошо видно (для сравнения я взял негармоничную пару — 300 и 520 Гц):
Кроме того, гармоники любой отдельной ноты содержат в себе чистые интервалы. Например, третья гармоника любой ноты в 3/2 раза выше по частоте, чем вторая гармоника этой же ноты. Так что чистые интервалы происходят из базовых физических свойств звука.
Самый простой из чистых интервалов — это октава: 2/1. Она обладает важным свойством — если взять две ноты с разницей в октаву, то ВСЕ гармоники верхней ноты будут совпадать с чётными гармониками нижней (пример — в предыдущей сноске). Такие ноты максимально «сливаются» вместе и воспринимаются как одна. Поэтому они и назваются одинаково (До и следующая До). Сравните одну и ту же мелодию сыгранную большими терциями, квинтами и октавами, и всё станет понятно:
В посте я буду говорить про разные квинты, терции, и т.д. Но величина октавы будет всегда одна — 2/1.
—
Когда одновременно звучат колебания близкой частоты (например, 200 и 202 Гц), между ними возникают так называемые биения — звук «плавает» или «дрожит» оттого что колебания медленно сдвигаются по фазе относительно друг друга.
Поэтому если интервал между двумя нотами не совсем чистый, но близок к чистому, то биения возникнут между некоторыми гармониками этих нот. Для примера — квинта, которая немного больше чистой:
200, 400, 600, 800, 1000, 1200,…
302, 604, 906, 1208,…
Чем сильнее интервал отклоняется от чистого, тем чаще биения и тем «нестабильнее» он звучит.
—
Ещё интервалы измеряют в центах. Цент — это очень маленький интервал: 1,0005777895… (корень 1200-й степени из 2х). Это одна сотая современного полутона. Он понадобится, чтобы оценить мелкие различия между интервалами.
Вот пример, который поможет ощутить масштабы цента:
—
Последнее примечание: из интервалов я буду говорить только о секундах, терциях и квинтах, потому что интервалы, которые являются обращениями друг друга, ведут себя совершенно аналогично. Например, если в каком-то строю терция C-E получается немного больше, чем чистая терция, то секста E-C — ровно настолько же меньше. И так далее: с квартами дела обстоят так же, как с квинтами, а с септимами — так же, как с секундами.
Невозможность совершенства
Если посмотреть на таблицу частот разных нот, видно, что чистых интервалов там практически нет. Между нотами A3 и A4 одна октава разницы (220 Гц * 2=440 Гц). А, скажем, нота E4, которая на квинту выше A3, имеет частоту не 330 Гц (220 Гц * 3/2), а немного меньше.
Всё дело в том, что с чистыми интервалами есть проблема: они в очень многих случаях НЕ СХОДЯТСЯ друг с другом.
Например, возьмём ноту До (C), прибавим к ней две октавы и одну большую терцию. То есть два раза удвоим частоту, а потом умножим на 5/4.
Получилась нота Ми (E) через две октавы.
Теперь отложим от той же самой До четыре квинты вверх. То есть, четыре раза умножим частоту на 3/2. Получилась та же самая нота Ми.
Или не та же самая?
В первом случае частота Ми ровно в 5 раз выше, чем До: 2*2*5/4=5.
А во втором — в 81/16 раз выше (3/2*3/2*3/2*3/2=81/16). То есть в 5,0625 раз выше.
Получается, что две октавы плюс чистая большая терция не равны четырём чистым квинтам, из-за чего невозможно определить правильную частоту Ми относительно До. И таких расхождений много1.
—
Ещё пример: простая мелодия, которая начинается с До и движется так: квинта вверх, кварта вниз, квинта вверх, кварта вниз, большая терция вниз — вернулись в ту же До.
НО! Если все эти интервалы чистые, то До в конце мелодии получается выше, чем До, которая была в начале! А именно — в 81/80 раз выше: 3/2*3/4*3/2*3/4*4/5=81/80, и не равно 1. Повторим эту мелодию ещё раз, начав с новой До — и До станет выше почти на полтона. Вот, послушайте (в конце я для наглядности повторяю изначальную До):
Чтобы этого сдвига не происходило, придётся, например, пожертвовать чистотой большой терции и немного её увеличить.
А вот здесь, с 4:15, очень наглядно показывают этот сдвиг на примере аккордов.
—
Из всего этого ясно, что для построения нотной системы неизбежно придётся идти на какие-то компромиссы. Например, чтобы в предпоследнем примере получались не разные Ми, а одинаковые, придётся либо сделать квинту немного меньше, чем 3/2, либо сделать большую терцию немного больше, чем 5/4, либо сделать понемножку и то и другое. Именно это и происходило, когда музыканты пытались найти компромисс. В одни исторические периоды предпочтение отдавали чистой квинте, в другие — чистой терции.
Вот теперь можно рассказать про несколько исторических строёв.
Пифагоров строй
Начнём с того, что строй этот создал не Пифагор. Насколько я понимаю, строй оформился в период поздней античности, а название получил потому что был основан на идеях пифагорейцев, которым очень нравилась идея гармонии чисел.
Пифагоров строй — это звукоряд, построенный на двух самых простых соотношениях — октаве и чистой квинте. Берём основную ноту, откладываем от неё вверх и вниз цепочку квинт и таким образом находим частоты для всех остальных нот.
Начнём, например, с До. Прибавим к ней чистую квинту и получим Соль, частота которой в 3/2 раза выше До. Прибавим к этой Соль чистую квинту — получим Ре, частота которой в 3/2 выше, чем у Соль, и в 9/4 раз выше, чем у исходной До (3/2*3/2). Дальше — Ля, с частотой в 27/8 выше исходной До, и так далее.
В обратную сторону от До тоже можно откладывать квинты. Получится Фа, с множителем 2/3, Си-бемоль с множителем 4/9, и так далее.
На верхней клавиатуре изображены несколько первых шагов процесса:
На нижней клавиатуре полученные ноты собраны в одну октаву с До. Например, Ре (9/4), которая получилась из двух квинт, мы понизили на октаву (=поделили на 2), и получилась Ре, которая на тон выше исходной До: 9/8. Ля тоже понизим на октаву — получится 27/16. Ми понизим на две октавы, Фа повысим на октаву, и так далее.
Если начать с Ре и отложить от неё по три квинты в обе стороны, получится 7 нот (F-C-G-D-A-E-B), составляющих До-мажор. Переместим их в одну октаву и получим такие соотношения:
| Нота | C | D | E | F | G | A | B | C | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Соотношение с первой С | 1/1 | 9/8 | 81/64 | 4/3 | 3/2 | 27/16 | 243/128 | 2/1 | ||||||||
| Соотношение между соседними нотами | 9/8 | 9/8 | 256/243 | 9/8 | 9/8 | 9/8 | 256/243 | |||||||||
Если продолжить процесс дальше и отложить от Ре по шесть квинт в обе стороны, то получится такой ряд нот:
| Нота | Соотношение с D |
| Ab | 1024/729 |
| Eb | 256/243 |
| Bb | 128/81 |
| F | 32/27 |
| C | 16/9 |
| G | 4/3 |
| D | 1 |
| A | 3/2 |
| E | 9/8 |
| B | 27/16 |
| F# | 81/64 |
| C# | 243/128 |
| G# | 729/512 |
Получилось 13 нот, причём ноты Ab и G# получились разными: соотношение 1024/729 близко, но не равно 729/512 (1,40466…<1,423828…).
Так проявляется ещё одна проблема чистых интервалов: 7 чистых октав не равны 12 чистым квинтам. 7 октав — это 128/1. А 12 чистых квинт — это 531441/4096, то есть 129,746…
Наша пифагорова G# ровно на 12 квинт выше, чем Ab, поэтому когда мы их приводим в одну октаву, получается не одна нота а две близких.
Разница между ними называется Пифагоровой коммой. Это небольшой интервал, примерно 23,46 цента, то есть чуть меньше четверти нынешнего полутона.
Нам нужно 12 нот, поэтому отбросим Ab и оставим G#.
Можно, конечно, ввести в наш строй обе ноты — Ab и G#, но это во-первых, непрактично на многих инструментах2, а во вторых, не решит проблему полностью. Например, мы не сможем сыграть чистую квинту от G#, потому что ноты D# у нас нет, а если играть вместо неё Eb, квинта будет не чистая, а опять же уменьшенная на пифагорову комму.А если продолжать добавлять ноты, то придётся строить инструмент с такой, например, клавиатурой:
Если играть в До-мажоре или каких-то близких тональностях, достаточно будет среднего ряда клавиш. А вот чистую квинту от G# придётся играть так: G# на средней клавиатуре и D# на верхней. И вообще: в тональностях, в которых много «чёрных клавиш» часть нот придётся брать на одной клавиатуре, часть на другой.
И теперь одна квинта из двенадцати не чистая, а на пифагорову комму меньше чистой.
Эту квинту назвали «волчьей» квинтой. «Биения», которые возникают в «волчьей» квинте, напомнили кому-то волчий вой, отсюда название.
Одна плохая квинта из двенадцати — ещё не беда (в конце концов, мы можем избегать игры в тональностях, в которых эта квинта встречается — а это половина всех тональностей). Беда в том, что ВСЕ интервалы в пифагоровом строе получены из квинт, а значит — любой интервал, в котором участвует волчья квинта, уменьшается или увеличивается на пифагорову комму. Например, большая секунда получается из двух квинт, поэтому из 12-ти больших секунд 10 штук получаются чистыми, а две (C#-D# и G#-A#) — уменьшены на пифагорову комму. Септимы D#-C# и A#-G#, соответственно, увеличены на пифагорову комму. С другими интервалами такая же беда, только там изменённых интервалов получится ещё больше. Например, большая терция строится из четырёх квинт, поэтому из 12-ти больших терций 8 будут «обычного» размера, а 4 штуки — на пифагорову комму меньше.
—
Ещё одна проблема с пифагоровым строем — терции в нём серьёзно отличаются от чистых. Пифагорова большая терция — это «четыре чистых квинты минус две октавы». То есть, 3/2*3/2*3/2*3/2:4. Получается 81/64, а это заметно больше, чем чистая большая терция 5/4 (1,265625 > 1,25).
То же самое с малой терцией. Пифагорова малая терция — это «две октавы минус три чистые квинты», или 2/3*2/3*2/3*4. Получается32/27, и это заметно меньше, чем чистая малая терция 6/5 (1,185185… < 1,2).
| Малая терция | Большая терция | |
| Чистая | 6:5 315.64 центов | 5:4 386.31 центов |
| Пифагорова | 32:27 294.13 цента | 81:64 408 центов |
| Разница | на 21.51 цент меньше | на 21.51 цент больше |
Интервал, на который они отличаются, называется синтонической коммой. Её размер — 81:80 или 21.51… цент (примерно одна пятая нынешнего полутона). С этой коммой мы уже встречались в начале текста — именно настолько повышалась До в мелодии, состоящей из чистых интервалов — и встретимся ещё.
Пифагоровы терции звучат для нас вполне норм, потому что они близки к нашим нынешним терциям (которые тоже совсем нечистые, но мы привыкли). Но средневековым музыкантам это было не норм, поэтому терция в то время не использовалась как основа гармонии.
Пифагоров строй использовали примерно до 15 века. Потом его стали модифицировать, чтобы как-то поправить ситуацию с терциями.
Среднетоновый строй на 1/4 коммы
В 16 веке появился новый строй — среднетоновый на 1/4 коммы. Он устроен так же как пифагоров, только размер всех квинт уменьшен ровно настолько, чтобы большая терция стала чистой.
Вот как это работает. Пифагорова большая терция создаётся с помощью четырёх квинт: строим цепочку квинт С-G-D-A-E, понижаем полученную E на две октавы, и получаем терцию C-E, которая, как я показывал выше, не чистая, а на синтоническую комму больше чистой. Если уменьшить каждую квинту на 1/4 синтонической коммы, то терция, полученная из четырёх квинт, уменьшится на одну синтоническую комму, а значит, станет равна чистой терции. При этом квинта перестала быть чистой, но и не сильно пострадала — уменьшилась всего на 5 центов.
Все остальные интервалы тоже получены из квинты, поэтому их размеры тоже изменились. Одним это пошло на пользу, другим — нет. Например, малая терция стала почти чистой (всего на 6 центов меньше чистой), большая секунда стала на 11 центов меньше чистой, и так далее. Но в целом интервалы получились приемлемые.
К сожалению, проблемы с «волчьей квинтой» и прочими волчьими интервалами здесь ещё хуже, чем в пифагоровом строе. В пифагоровом строе «волчья квинта» на пифагорову комму меньше чистой, а в среднетоновом — на полторы пифагоровы коммы больше. Поэтому одна квинта из двенадцати у нас получается безобразно, на 35 центов, увеличенной. Две большие секунды из двенадцати получаются безобразно увеличенными (на 30 центов больше чистой). 9 из 12-ти малых терций почти чистые, зато остальные три — на 47(!!) центов уменьшены. 8 из 12-ти больших терций совершенно чистые, зато остальные на 41(!) цент увеличены.
В итоге, при игре в тональностях, недалеко отходящих от основной ноты, мы получаем совершенно чистые большие терции и приемлемо чистые остальные интервалы. А вот в каком-нибудь Фа-диез мажоре будет много фальшивящих интервалов.
Одна и та же последовательность аккордов в разных тональностях. Начинаем с базового До мажора и сдвигаемся каждый раз на тон выше. Где-то в середине — там, где аккорды максимально далеки от базовой тональности — можно услышать некую фальшь.
Среднетоновый строй на 1/4 коммы был основным строем в европейской музыке до начала 18-го века, а на многих органах — до середины 19-го века.
Натуральный строй
Другая идея, которая возникла в конце 16 века — построить такой звукоряд, чтобы интервалы были максимально чистыми хотя бы в пределах одной тональности.
Возьмём ноту F и прибавим к ней чистую большую терцию, получив ноту A. К этой A прибавим чистую малую терцию и получим C. Продолжим чередовать большие и малые терции пока не получится 7 нот:
| Нота | F | A | C | E | G | B | D | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Соотношение | 5:4 | 6:5 | 5:4 | 6:5 | 5:4 | 6:5 | ||||||||
Чистая большая терция и чистая малая терция дают в сумме чистую квинту (5/4*6/5=3/2; хоть где-то эти чистые интервалы сходятся!), поэтому квинты F-C, A-E, C-G, E-B и G-D здесь получились чистые.
Соберём эти ноты в одну октаву и получим звукоряд До-мажор — CDEFGABC, в котором почти все интервалы чистые. Чистыми получились все большие терции (CE, FA и GB) и три из четырёх малых терций (E-G, A-C и B-D). Однако, полного совершенства не получилось даже здесь: квинта D-A и малая терция D-F на пифагорову комму меньше, чем чистые.
Кроме того, получились две разных больших секунды. Одна — C-D, F-G и A-B — такая же как в пифагоровом строе (9:8 или 204 цента). Вторая — D-E и G-A — на пифагорову комму меньше (10:9 или 182 цента). Малые секунды E-F и B-C одинаковые — 15:16 (112 центов).
Итак, у нас есть 7 «белых» нот, интервалы между которыми чисты настолько, насколько это возможно. Добавим к ним 5 оставшихся «чёрных» нот (например, вычтем квинту из F и получим Bb, и так далее).
Получился строй, в котором интервалы в «исходной» тональности (До-мажор) и близких к ней тональностях — в основном чистые. Но если фальши убавилось в одном месте, её должно прибавиться где-то ещё, поэтому интервалы в далёких от До-Мажора тональностях будут сильно фальшивить.
Сейчас в чистом строю играют только музыканты, аутентично исполняющие древнюю музыку. А с другой стороны, инструменты, у которых высота нот не фиксированная (вокал, безладовые струнные, часть духовых), на практике часто склоняются к чистым интервалам. Например, певцы, поющие терцию, могут подстраиваться друг под друга так, чтобы исчезли «биения».
Все терции и квинты в натуральном До мажоре.
«Хорошо темперированные» строи
В конце 17-начале 18 века появились строи, разработанные так, чтобы можно было играть во всех или почти всех тональностях с минимальной «лажей» в интервалах. Идея была в том, чтобы понижать не все квинты, как в среднетоновом строе, а выборочно понижать часть из них.
Этих строёв было множество. Например, в одной из темпераций Веркмейстера пять квинт (C-G, D-A, E-B, F#-C#, and Bb-F) уменьшены на 1/3 коммы, две квинты (G#-D# и Eb-Bb) увеличены на 1/3 коммы, а остальные квинты — чистые.
В «хорошо темперированных» строях одни интервалы получаются чистыми, другие — почти чистыми, и лишь некоторые отклоняются сильно. В итоге стало возможно играть во всех тональностях без сильной фальши. Тональности получились разными — в одних было больше отклонений от чистых интервалов, чем в других, и распределение этих отклонений получалось разное. Если в нынешнем, равномерно темперированном строе перенести музыку в другую тональность, то она прозвучит точно так же (в том смысле, что соотношения между всеми нотами останутся такими же). А в «хорошо темперированном» строе от этого изменится «оттенок» музыки, потому что интервалы будут немного другими.
Здесь нельзя не упомянуть «Хорошо темперированный клавир» — сборник произведений Баха, вышедший в 1722 году. Он состоит из произведений во всех 24-х тональностях (12 мажорных и 12 минорных). Название, скорее всего, отсылает к «хорошо темперированным» строям, тем более что и состав сборника как бы говорит: наконец-то появился строй, в котором можно играть во всех тональностях!
Бах был недоволен общепринятым тогда среднетоновым строем и настраивал свои инструменты как-то по своему. Неизвестно, какую именно темперацию он использовал. Некоторые музыковеды даже полагают, что строй Баха каким-то образом зашифрован в тринадцати петлях, нарисованных им на заглавии сборника:
Равномерно темперированный строй
Идея разбить октаву на 12 равных частей высказывалась с древних времён. Это решает проблему с несходящимся квинтовым кругом, делает все интервалы одинаковыми, а все тональности равноправными. Однако на практике её применять не спешили. Во первых, терции в этом строе почти такие же нечистые, как и в пифагоровом. Во-вторых, для расчётов соотношений между нотами нужна продвинутая математика — ведь всё основано на корне 12-й степени из двух. В-третьих, в эпоху «хорошо темперированных строёв» композиторам очень нравилось то, что у разных тональностей разный «оттенок» и характер.
В течение 19 века многие композиторы (например, Бетховен) начали широко применять в музыке модуляции в далёкие тональности, и идея о равноправности тональностей становилась всё более привлекательной.
Итак, берём октаву (2/1) и разбиваем её на 12 равных интервалов — полутонов, из которых будем составлять все остальные интервалы (большая терция — это 4 полутона, чистая квинта — 7 полутонов, и так далее). Каждый полутон равняется корню 12-й степени из двух (21/12) — примерно 1.059463. Теперь между двумя соседними нотами ВСЕГДА интервал в 100 центов. Все терции одинаковы по размеру, все квинты одинаковые, и так далее.
В этом строю нет ни одного чистого интервала кроме октавы — все остальные определяются не то чтобы непростыми дробями (как в пифагоровом строе), а вообще иррациональными отношениями. Очень близки к чистым оказались квинта (выше чистой всего на 2 цента), и большая секунда (ниже чистой всего на 4 цента). А вот терциям не повезло. Малая терция получилась на 16 центов меньше чистой, а большая — на 14 центов больше. Это серьёзная разница, приводящая к заметным биениям:
Тем не менее к 20 веку практически все музыканты перешли на этот строй (а лютни и гитары на нём всегда и были). Равноправие тональностей и полное отсутствие «волчьих» интервалов оказалось важнее, чем нечистые терции.
В следующей части поста — ещё аудиопримеры и таблицы с интервалами.
—
1 — Например:
Три чистые большие терции не равны октаве, а меньше: 5/4*5/4*5/4=1,953125.
Четыре чистые малые терции не равны октаве, а больше: 6/5*6/5*6/5*6/5=2,0736
Шесть чистых тонов не равны октаве, а больше: 9/8*9/8*9/8*9/8*9/8*9/8=2,027286529541015625.
2 — тем не менее были попытки решить проблему хотя бы частично и существовали инструменты, на которых одна, две или три из чёрных клавиш в каждой октаве раздвоены — например, Ля-бемоль и Соль-диез.
Например, вот этот клавесин, с 14 клавишами на октаву:
Или этот, с 19-ю клавишами на октаву:
Задача 68. Просим к роялю!. Раритетные издания. Наука и техника
Пётр Маковецкий. Смотри в корень! Сборник любопытных задач и вопросов
А.
Перед вами хорошо настроенное пианино. Вам разрешается трогать клавиши, но, естественно, запрещается перестраивать струны, передвигать по ним порожки и вообще забираться внутрь инструмента.
Можно ли заставить струну «до» первой, октавы звучать, как «соль» второй?
Б.
Прежде всего условимся в обозначениях: все ноты первой октавы будем писать с приставкой 1 (до-1, ре-1, фа-диез-1 и т.д.), второй – с приставкой 2 (си-2) и т.д.
Если читатель не музыкант, то он убежденно заявляет, что поскольку высота тона струны определяется ее длиной, толщиной и натяжением, то, не перестраивая струну, нельзя заставить до-1 звучать иначе, чем до-1. Таковы законы физики, и тут ничего не поделаешь. Разве только вынести пианино на трескучий мороз, тогда струна при остывании укоротится, сильнее натянется и тон ее повысится.
Чтобы ваше мнение о возможностях струны изменилось в благоприятную сторону, решите две задачи полегче.
1. Частота, соответствующая до-1, равна 261,63 Гц. Чему равны частоты второй, третьей, четвертой гармоник этой струны? Можете ли вы назвать ноты, соответствующие этим гармоникам? Если не можете, то даем подсказку: увеличение частоты вдвое повышает любую ноту на октаву. Поскольку в октаве 12 полутонов, то повышение на полтона (при равномерно темперированной шкале) увеличивает частоту в 21/12 раз, на тон – в (22)1/12, на полтора тона – в (23)1/12 и т.д. Впрочем, чтобы уж совсем избавить вас от вычислений, приводим таблицу абсолютных частот всех нот первой и второй октав (в графе f / f1 – относительные частоты, т.е. числа, показывающие, во сколько раз частота f выше частоты f1 = 261,63 Гц).
Таблица 4
| Нота | Октава 1 | Октава 2 | ||
| f | f / f1 | f | f / f1 | |
| До | 261,6 | 1 | 523,2 | 2 |
| До-диез | 277,2 | 1,06 | 554,4 | 2,12 |
| Ре | 293,7 | 1,12 | 587,3 | 2,24 |
| Ре-диез | 311,1 | 1,19 | 622,3 | 2,38 |
| Ми | 329,6 | 1,26 | 659,3 | 2,52 |
| Фа | 349,2 | 1,33 | 698,5 | 2,67 |
| Фа-диез | 370,0 | 1,41 | 740,0 | 2,83 |
| Соль | 392,0 | 1,50 | 784,0 | 3,00 |
| Соль-диез | 415,3 | 1,59 | 830,6 | 3,17 |
| Ля | 440 | 1,68 | 880 | 3,36 |
| Ля-диез | 466,2 | 1,78 | 932,3 | 3,56 |
| Си | 493,9 | 1,89 | 987,8 | 3,78 |
Частота ноты ля-1 написана без знаков за запятой, потому что условились считать ее в точности равной 440 Гц, а остальные ноты получать из нее путем вычислений.
2. Освободите до-1, т.е. осторожно, без звука, нажмите на соответствующую клавишу. При этом демпфирующий (заглушающий) молоточек поднимается. Ударьте по до-2 и через секунду-другую отпустите ее клавишу. Почему до-2 продолжает звучать? Отпустите до-1. Почему перестала звучать до-2?
В.
Рассмотрим сначала вспомогательные задачи.
Рис. 87. Колебания струны
1. Если бы струна колебалась так, как показано на рис. 87, а, то она излучала бы чистый тон, т.е. колебание единственной частоты. Чистый тон сух и не очень приятен. Поэтому для музыки большая удача, что струна одновременно совершает несколько видов колебаний. Она одновременно колеблется всей длиной (рис. 87, а, первая гармоника), двумя половинками (рис. 87, б, вторая гармоника), тремя третями (рис. 87, в, третья гармоника), четырьмя четвертями (рис. 87, г) и т.д. Частота колебаний обратно пропорциональна длине соответствующей волны. Если рис. 87, а, б, в и г изображают струну до-1, то эти гармоники имеют частоты f1 = 261,6 Гц, 2f1 = 523,2 Гц, 3f1 = 784,9 Гц и 4f1 = 1046,5 Гц соответственно. Это до-1, до-2, почти точно соль-2 (точное значение 784,0 Гц) и до-3. С увеличением номера гармоники ее интенсивность A, как правило, уменьшается (рис. 88, а).
Рис. 88. Спектр нотного ряда с равномерной шкалой
2. Ударив по до-2, мы возбудили колебания на частоте f2 = 2f1 = 523,2 Гц и ее гармониках f3 = 2f2 = 4f1 = 1046,5 Гц и др. Струна до-1 освобождена от демпфера и могла бы начать колебаться, если бы ее кто-нибудь возбудил. Этим возбудителем и будет звучащее до-2. Правда, вся струна до-1 настроена на октаву ниже, т.е. не находится в резонансе с до-2, но зато ее половинки (рис. 87, б) могут поддержать колебания на частоте до-2. Иными словами, струна до-2 возбудит в струне до-1 вторую гармонику, не возбуждая первой (!). Вторая гармоника до-2 возбудит в до-1 ее четвертую гармонику (2f2 = 4f1), и т.д. Струна до-1 будет излучать только четные свои гармоники. Отпустив клавишу до-2, мы заглушаем струну до-2 и прекращаем ее колебания. Но часть энергии ее первой гармоники передана второй гармонике струны до-1. Поэтому мы продолжаем слышать до-2: эта нота исходит от струны до-1. В том, что это именно так, легко убедиться; отпустим клавишу до-1, и нота до-2 прекратится!
Итак, можно заставить струну звучать не на той ноте, на которой она официально обязана звучать. Теперь вы наверняка сумеете сами решить первоначальную задачу. Для этого следует перестать читать и подумать. Вот это решение.
Чтобы заставить до-1 звучать, как соль-2, нужно возбудить ее третью гармонику (не возбуждая первой и второй, иначе эти сильные гармоники заглушат слабую третью). Для этого нужно освободить до-1 и ударить соль-2 (которая, как мы выяснили ранее, и является третьей гармоникой до-1). Отпустив соль-2, мы услышим ноту соль-2 теперь уже от струны до-1.
Весьма любопытно, что извлечь ноту соль-2 из струны до-1 можно и без участия струны соль-2. Вместо нее можно использовать струну соль-1. Как же при этом произойдет возбуждение струны до-1? Вторая гармоника струны соль-1 возбудит третью гармонику струны до-1:
2fсоль-1 = 2·392 = 784 ≈ 3·261,6 = 3fдо-1.
На рис. 87, д показана первая гармоника струны соль-1, на рис. 87, е – вторая. Видно, что колебания на рис. 87, е находятся в резонансе с колебаниями на рис. 87, в, изображающем третью гармонику струны до-1. Первая же и вторая гармоники струны до-1 не будут возбуждены: в спектре струны соль-1 (рис. 88, б) нет совпадающих с ними гармоник. Однако шестая гармоника до-1 будет возбуждена с помощью четвертой гармоники соль-1, девятая – с помощью шестой, и т.д.
Если вы как следует прочувствовали эти диковинные вещи, то вы неминуемо задержитесь у пианино на десяток минут и найдете у него самые невероятные возможности. Так, освободив соль малой октавы (соль-M, f = 392/2 = 196 Гц) и ударив по ми-1, вы услышите си-2! Это значит, что третья гармоника струны ми-1 возбудит пятую гармонику струны соль-M:
5f /соль-M = 5·196 = 980 ≈ 3fми-1 = ;3·329,6 = 988,8 ≈ fси-2 = 987,8.
Из каждой струны можно извлечь только те ноты, которые являются гармониками основного тона. С помощью струны соль-1 можно извлечь из струны до-1 звуки соль-2, соль-3 (см. рис. 88, а и б), с помощью до-M можно извлечь до-1, до-2, до-3, с помощью до-1 – слабый ми-3 (как видно из рисунка, пятая гармоника до-1 почти точно совпадает с точкой, изображающей ми-3). Но нет никакого способа (кроме уже упомянутого мороза) заставить струну до-1 звучать, как ре-1, ре-диез-1, ми-1 и т.д., так как в пределах первой октавы струна до-1 содержит единственную гармонику. Однако в пределах второй октавы струна до-1 дает уже две гармоники, в пределах третьей–четыре, четвертой–восемь, пятой– шестнадцать, шестой – тридцать две! Поскольку в октаве всего двенадцать нот, то на каждую из них придется почти по три гармоники от до-1. Следовательно, струна до-1 принципиально могла бы дать любую ноту шестой октавы. Но для этого пришлось бы возбудить, например, сороковую гармонику струны до-1. Однако амплитуда ее так мала, что столь высокую гармонику обычно услышать не удается.
На рис. 88, а и б ось частот имеет равномерный масштаб. На рис. 88, в изображена клавиатура пианино так, чтобы каждая клавиша заняла своё место на оси частот. Поскольку повышение тона на октаву требует удвоения частоты, то при равномерной шкале частот шкала нот (клавиатура) будет неравномерной. Наоборот, если в привычном масштабе изобразить клавиатуру (рис. 89), то неравномерной окажется шкала частот (логарифмический масштаб). Из рис. 89 особенно хорошо видно, что на каждую новую октаву приходится вдвое больше гармоник струны до-1, чем на предыдущую.
Рис. 89. Спектр нотного ряда с логарифмической шкалой
Описанное в задаче явление можно обнаружить и на гитаре. Роль демпфирующих молоточков должны выполнять пальцы левой руки. Известный гитаристам прием извлечения так называемых флажолетт имеет прямое отношение к нашей задаче.
• Задача 69. Звезда и спичка
• Оглавление
Дата публикации:
10 июля 2004 года
теоретическое введение в акустику и оцифровку звука
Про такой сервис, как Shazam, слышали многие — он позволяет, прослушав музыкальный трек всего несколько секунд, практически гарантированно определить его название. С учетом того, что в библиотеке Shazam находится больше миллиона треков, это кажется чем-то из раздела фантастики, однако, очевидно, этому есть научное объяснение, и в этом цикле статей мы и поговорим, как этот сервис работает.
Оригинал статьи можно почитать здесь, я лишь ее перевел и несколько адаптировал для более простого понимания. Также я решил разбить эту статью на несколько частей: в начале будет теория — что такое, собственно, звук, как он записывается и что такой аналоговый и цифровой сигналы. В дальнейшем будет введение в оцифровку и описание таких понятий, как квантование и модуляция. Ну и под конец, на основе всего этого, будет объяснено, как же работает сам сервис Shazam. Если вы хорошо знаете физику — теоретические части статьи вы можете пропустить, ну а всем другим — welcome.
Музыка и физика
Звук — это вибрация (вообще говоря — упругая волна, но у нас же научно-популярная статья, верно?), которая может распространяться через любую среду (воздух, воду, даже почву и металлы) и может быть «расшифрована» нашими ушами. Например, когда вы слушаете музыку, наушники (или колонки) производят вибрации, которые распространяются по воздуху до тех пор, пока не достигнут ваших ушей. Свет также является волной, однако мы его не слышим из-за того, что наши уши не приспособлены для его восприятия — однако, к примеру, глаза — приспособлены.
Любая волна может быть с любой точностью аппроксимирована (приближена) совокупностью синусоидальных волн, что здорово упрощает нам жизнь (почему — объясню ниже).
Чистые тона против реальных звуков
Чистый тон — это звук, построенный на гармонических (синусоидальных) колебаниях. Синусоидальная волна характеризуется двумя параметрами:
- Частотой — количеством колебаний в секунду, за единицу измерения принят Герц (Гц). К примеру, 100 Гц = 100 колебаний в секунду.
- Амплитудой (связанной с громкостью) — размер каждого колебания (громкость может измеряться в децибелах, но об этом ниже).
Вы можете проверить, насколько высокий звук вы можете услышать, с помощью, к примеру, такого ролика на YouTube — однако перед этим проверьте, поддерживают ли ваши наушники и звуковая карта возможность проигрывать высокие частоты вплоть до 20 кГц, ведь в противном случае вы можете наткнуться на предел оборудования, а не ваших ушей.
Наше восприятие громкости зависит от частоты чистого тона. Например, из двух чистых тонов с одинаковой амплитудой, но разной частотой (к примеру, 30 и 1000 Гц), нам будет казаться более громким тот тон, у которого частота выше. Для лучшего понимания этого факта можно почитать Википедию, мы же идем дальше.
На картинке ниже вы можете увидеть чистый тон с частотой в 20 Гц:
Как я уже писал выше, это — модель, таких волн в природе не существует. Однако любую волну можно разбить на несколько синусоидальных, с разными частотами и амплитудами. Разумеется, это опять же не будет точно соответствовать реальному звуку, но всегда можно добавлять еще волн до тех пор, пока разница не станет незаметной:
На картинке выше показана волна, уже более приближенная к реальной. В данном случае она состоит из 4-ех синусоид:
- Синусоидальная волна с частотой 20 Гц и амплитудой 1;
- Синусоидальная волна с частотой 40 Гц и амплитудой 2;
- Синусоидальная волна с частотой 80 Гц и амплитудой 1.5;
- Синусоидальная волна с частотой 160 Гц и амплитудой 1.
Музыкальные ноты
Если вы не учились в музыкальной школе, то сей раздел для вас будет немного трудным. Итак, вот так выглядит нотный стан:
Он представляет собой набор нот, которые расположены на линиях, чем выше — чем больше частота. Также различным типом кружков показывается длительность каждой ноты. В общем и целом — нам нотный стан не понадобится, он здесь просто для наглядности.
Все ноты делятся на октавы — в большинстве стран принято, что в каждой октаве по 7 нот: A, B, C, D, E, F, G (по-русски это Ля, Си, До, Ре, Ми, Фа, Соль). Октава пишется справа от ноты цифрой. Правило получения нот такое — частота одной и той же ноты в каждой следующей октаве удваивается. К примеру, До второй октавы (A2) имеет частоту 110 Гц. До третьей октавы (A3) уже имеет частоту в 220 Гц, 4-ой (A4) — уже 440 Гц. Многие инструменты могут воспроизвести в каждой октаве больше, чем 7 нот — эти «дополнительные» ноты называются полутонами.
Для 4-ой октавы («средняя» октава) ноты имеют следующие частоты:
- C4 (или До3) = 261,63 Гц
- D4 (или Ре3) = 293,67 Гц
- E4 (или Ми3) = 329,63 Гц
- F4 (или Фа3) = 349,23 Гц
- G4 (или Соль3) = 392 Гц
- A4 (или Ля3) = 440 Гц
- B4 (или Си3) = 493,88 Гц
Забавный момент: у наших ушей логарифмическая чувствительность — а это значит, что и между 32.7 Гц — 61.74 Гц (1-ая октава), и между 261.63 Гц — 466.16 Гц (4-ая октава), и между 2093-3951.07 Гц (7-ая октава) наши уши могут обнаружить одинаковое число нот.
Разумеется, должна быть калибровочная нота, и она есть — это A4 (Ля 3-ей октавы), 440 Гц — именно по ней калибруют акустическое оборудование и музыкальные инструменты.
Тембр
Одна и та же нота звучит по-разному, когда ее играет гитара, фортепиано, скрипка или поет певец. Причина в том, что каждый инструмент имеет собственный тембр для каждой ноты. Создаваемый каждым инструментом звук представляет собой множество частот, которые звучат как данная нота (научный термин — высота звука). Такой звук имеет основную частоту (самую низкую), и несколько обертонов (звуки с частотой, выше основной).
Большинство инструментов производят звуки, близкие к гармоническим — то есть для них обертоны являются кратными основной частоте, и называются гармониками. Например, чистые тона A2, A4 и A6 являются гармоничными (у них разница в частотах в 4 раза между соседними тонами), а вот A2, B3, и F5 — ангармоничны: обычно такие звуки производят ударные инструменты (тарелки или барабаны).
Наш мозг — удивительный прибор: высота звука (воспринимаемая нота) может отсутствовать в звуке, воспроизводимом инструментом. Например, если инструмент издает звук с чистыми тонами A4, A6 и A8, то мозг человека будет интерпретировать его как A2, тогда как самая низкая (основная) частота — это A4. Почитать об этом опять же можно в Википедии.
Спектрограмма
Зачастую песня исполняется сразу несколькими инструментами и певцами. Все эти инструменты создают комбинацию синусоид, а общая картина — еще большая комбинация. При этом ее… можно увидеть — для этого и создана спектрограмма. Она представляет собой трехмерный график, где по горизонтальной оси (X) отложено время, по вертикальной (Y) — частота чистого тона, по третьей оси (Z) — амплитуда волны в определенное время.
Например, спектрограмма фортепианного воспроизведения ноты C4 (с основной частотой 261.63 Гц), выглядит так:
Цветом показана амплитуда волны в дБ (об этом будет дальше). Так как фортепиано является гармоническим инструментом, то в записи явно видны частоты, выше чем 261 Гц у C4.
Еще одним интересным фактом является то, что интенсивность частот меняется во времени — это является особенностью инструмента и делает его уникальным. Поэтому если вы возьмете того же исполнителя, но замените музыкальный инструмент, то звук будет немного другой — с технической точки зрения, меняется огибающая звукового сигнала (которая является частью тембра).
На этом месте уже можно немного поговорить о том, как Shazam «снимает слепок» с композиции — как видно по спектрограмме, некоторые частоты (самые низкие) громче (а значит и важнее) других. Что, если мы будем отсекать все другие, для упрощения работы алгоритма?
Оцифровка
Если вы не любитель слушать музыку с виниловых пластинок, то, значит, вы используете какой-то из цифровых форматов (mp3, ogg, flac). Но вот когда артисты воспроизводят музыку, она аналоговая — то есть не представлена битами. И чтобы хранить такую музыку и воспроизводить на электронных устройствах, она оцифровывается — и о том, как это делается, мы поговорим ниже.
Дискретизация
Аналоговые сигналы являются непрерывными, то есть вы можете бесконечно уменьшать промежуток звучания сигнала, и вы каждый раз будете получать разный звук. Однако в цифровом мире мы не можем хранить бесконечное количество информации, поэтому тут приходится идти на хитрость и задавать минимальную единицу звучания — к примеру, 1 миллисекунду: в этот промежуток времени звук не может меняться. И это время уже гибко настраивается так, чтобы, с одной стороны, цифровая песня звучала как аналоговая, но, с другой стороны, так, чтобы трек весил не очень много. Представьте, к примеру, что в вашей любимой песне звук меняется только раз в пару секунд (технический термин — сглаженный звук). Узнаете ли вы ее? Вряд ли. С другой стороны, можно сделать это время в 1 наносекунду (10-9 с) — тогда качество будет отличным, но вот вес трека, увы, не порадует. За эту проблему поиска оптимальной единицы времени и отвечает дискретизация.
Стандартная дискретизация в цифровой музыке — это 44 100 единиц (выборок) в секунду. Откуда взялись эти 44.1 кГц? Ну, какой-то человек подумал, что число 44 100 отлично подходит, и все заверте… Шучу, конечно же нет.
Как мы помним, люди могут слышать звуки от 20 Гц до 20 кГц. В теореме Котельникова, она же теорема Найквиста-Шеннона (давайте я не буду ее приводить дословно, ладно?) говорится, что если вы хотите оцифровать сигнал от 0 до 20000 Гц, то вам потребуется не менее 40000 выборок в секунду. Основная идея тут в том, что синусоидальный сигнал на частоте F нуждается в определении не менее 2 точек за цикл, и, если частота вашей дискретизации не меньше, чем частота вашего сигнала, вы получите как минимум 2 точки за цикл исходного сигнала.
Попробуем понять это на примере. На картинке ниже звук с частотой в 20 Гц оцифровывается с частотой дискретизации в 40 Гц:
Синяя кривая представляет себе исходный синусоидальный сигнал с частотой в 20 Гц. Красные кресты — это наша выборка, дважды за цикл. Зеленая линия — интерполяция (приближение) исходного звука. Вы скажете — что-то не похоже это на наш звук. Так и есть, обычно частота дискретизации выше эдак на 3 порядка.
Чтобы было еще понятнее — ниже пример плохой выборки, когда звук с частотой в 20 Гц оцифровывается с частотой дискретизации в 30 Гц:
Тут, как видно, частота дискретизированного сигнала не совпадает с исходным сигналом — разница между ними в 10 Гц. И, если присмотритесь, то увидите, что один цикл в дисктеризированном сигнале представляет два цикла в исходном сигнале — это называется подвыборкой.
Также этот случай показывает кое-что еще: если вы хотите оцифровать сигнал между 0 Гц и 20 кГц, то вам необходимо перед этим убрать из него все частоты выше 20 кГц и ниже 0 Гц — в противном случае, эти частоты преобразуются в частоты между 0-20000 Гц и, следовательно, добавят нежелательные звуки (это называется наложением спектров).
Подводя итог: если вы хотите качественное преобразование аналоговой музыки в цифровую, то вы должны записывать ее с выборкой не менее 40000 единиц в секунду. HIFI-корпорации (например, Sony) выбрали частоту в 44.1 кГц еще в 80-ых, потому что она была выше необходимых 40 кГц и совместима с форматами NTSC и PAL. Существуют и другие стандарты — к примеру, 48 кГц (Blueray), 96 и 192 кГц, но, если вы не профессионал и не аудиофил, то, скорее всего, вы слушаете музыку в 44.1 кГц.
На этом мы, пожалуй, закончим сегодняшнюю часть статьи. В следующей части будет квантование, модуляция и дискретное преобразование Фурье (не пугайтесь — там не будет ничего сложного). Ну а после этого мы уже будем готовы посмотреть, как именно работает Shazam.
Ноты с частотой
Вот таблица с частотами в Гц музыкальных звуков, охватывающая полный диапазон всех обычных музыкальных инструментов, о которых я знаю, а также некоторые из них. Он использует равномерную темперированную шкалу с A = 440 Гц.
| C | C # | D | Eb | E | F | F # | G | G # | A | Bb | B | B | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 16.35 | 17,32 | 18,35 | 19,45 | 20,60 | 21,83 | 23,12 | 24,50 | 25,96 | 27,50 | 29,14 | 30,87 | |
| 1 | 32,70 | 34,65 | 36,71 | 38,89 | 41,20 | 43,65 | 46,25 | 49,00 | 51,91 | 55,00 | 58,27 | 61,74 | |
| 2 | 65.41 | 69,30 | 73,42 | 77,78 | 82,41 | 87,31 | 92,50 | 98,00 | 103,8 | 110,0 | 116,5 | 123,5 | |
| 3 | 130,8 | 138,6 | 146,8 | 155,6 | 164,8 | 174,6 | 185,0 | 196,0 | 207,7 | 220,0 | 233,1 | 246,9 | |
| 4 | 261.6 | 277,2 | 293,7 | 311,1 | 329,6 | 349,2 | 370,0 | 392,0 | 415,3 | 440,0 | 466,2 | 493,9 | |
| 5 | 523,3 | 554,4 | 587,3 | 622,3 | 659,3 | 698,5 | 740,0 | 784,0 | 830,6 | 880,0 | 932,3 | 987,8 | |
| 6 | 1047 | 1109 | 1175 | 1245 | 1319 | 1397 | 1480 | 1568 | 1661 | 1760 | 1865 | 1976 | |
| 7 | 2093 | 2217 | 2349 | 2489 | 2637 | 2794 | 2960 | 3136 | 3322 | 3520 | 3729 | 3951 | |
| 8 | 4186 | 4435 | 4699 | 4978 | 5274 | 5588 | 5920 | 6272 | 6645 | 7040 | 7459 | 7902 |
Номер октавы находится в левом столбце, поэтому, чтобы найти частоту среднего C, который является C4, посмотрите вниз столбец «C», пока не дойдете до строки «4»: таким образом, средний C равен 261.6 Гц.
Калькулятор частоты нот и проигрыватель
Вот утилита любезно предоставлено Колином Кроули, который будет вычислять частоты нот и может обрабатывать настройки, отличные от A = 440 Гц.
Он также может играть ноты, поэтому полезен в качестве справочника по настройке.
Работает в Windows и Linux. Воспроизведение нот может не работать в Safari на Mac, хотя Firefox или Chrome на Mac подойдут.
Некоторые особые примечания
Средний C равен C4 = 261.6 Гц
Стандартный камертон A составляет A4 = 440 Гц
Диапазон фортепиано от A0 = 27,50 Гц до C8 = 4186 Гц
Гитарные струны: E2 = 82,41 Гц, A2 = 110 Гц, D3 = 146,8 Гц, G3 = 196 Гц, B3 = 246,9 Гц, E4 = 329,6 Гц
Басовые струны (5-я струна) B0 = 30,87 Гц, (4-я струна) E1 = 41,20 Гц, A1 = 55 Гц, D2 = 73,42 Гц, G2 = 98 Гц
Струны мандолины и скрипки: G3 = 196 Гц, D4 = 293,7 Гц, A4 = 440 Гц, E5 = 659,3 Гц
Струны для альта и банджо тенор: C3 = 130,8 Гц, G3 = 196 Гц, D4 = 293,7 Гц, A4 = 440 Гц
Струны для виолончели — C2 = 65.41 Гц, G2 = 98 Гц, D3 = 146,8 Гц, A3 = 220 Гц
Coda
Имейте в виду, что здесь все связано с равномерно темперированной (также известной как равномерный темперированной) шкалой, где октава — это соотношение частот ровно два, а полутон — это соотношение частот точно корня двенадцатой степени из двух. Однако в реальном мире можно использовать много разных темпераментов — см. en.wikipedia.org/wiki/Musical_temperament — и октавы тоже могут различаться по размеру, см. en.wikipedia.org/wiki/Stretched_octave.
Также мы называем среднюю C «C4»: это самая распространенная октавная нумерация, но некоторые люди называют среднюю C «C3» или даже «C5».
Порекомендуйте эту страницу другим в этих социальных сетях:
Основные частоты нот в западной музыке
В главе 3 «Аудиторной нейробиологии» очень подробно обсуждаются интервалы высоты тона, используемые в западной музыке. Для удобства ниже приведена таблица основных частот для гаммы с равным темпом, скопированная с http://www.phy.mtu.edu/~suits/notefreqs.html.
По соглашению A 4 = 440 Гц
Ноты разделены полутоновыми интервалами.В каждой октаве 12 полутонов, а основные частоты разделены логарифмически, поэтому основная частота каждой ноты в 2 (1/12) = 1,0595 раз больше предыдущей частоты.
Значения длины волны предполагают скорость звука = 345 м / с
(«Средний C» — C 4 )
| Примечание | Частота (Гц) | Длина волны (см) |
|---|---|---|
| К 0 | 16.35 | 2109,89 |
| C # 0 / D b 0 | 17,32 | 1991,47 |
| Д 0 | 18,35 | 1879,69 |
| D # 0 / E b 0 | 19,45 | 1770. |
| E 0 | 20.60 | 1670. |
| Факс 0 | 21.83 | 1580. |
| F # 0 / G b 0 | 23,12 | 1490. |
| G 0 | 24,50 | 1400. |
| G # 0 / A b 0 | 25,96 | 1320. |
| А 0 | 27,50 | 1250 |
| A # 0 / B b 0 | 29.14 | 1180. |
| Б 0 | 30,87 | 1110. |
| К 1 | 32,70 | 1050. |
| C # 1 / D b 1 | 34,65 | 996. |
| Д 1 | 36,71 | 940. |
| D # 1 / E b 1 | 38.89 | 887. |
| E 1 | 41,20 | 837. |
| Факс 1 | 43,65 | 790. |
| F # 1 / G b 1 | 46,25 | 746. |
| G 1 | 49,00 | 704. |
| G # 1 / A b 1 | 51.91 | 665. |
| А 1 | 55,00 | 627. |
| A # 1 / B b 1 | 58,27 | 592 |
| Б 1 | 61,74 | 559. |
| К 2 | 65,41 | 527. |
| C # 2 / D b 2 | 69.30 | 498. |
| Д 2 | 73,42 | 470. |
| D # 2 / E b 2 | 77,78 | 444. |
| E 2 | 82,41 | 419. |
| Факс 2 | 87,31 | 395. |
| F # 2 / G b 2 | 92.50 | 373. |
| Г 2 | 98,00 | 352. |
| G # 2 / A b 2 | 103,83 | 332. |
| А 2 | 110,00 | 314. |
| A # 2 / B b 2 | 116,54 | 296. |
| Б 2 | 123.47 | 279. |
| К 3 | 130,81 | 264. |
| C # 3 / D b 3 | 138,59 | 249. |
| Д 3 | 146,83 | 235. |
| D # 3 / E b 3 | 155,56 | 222. |
| E 3 | 164.81 | 209. |
| Факс 3 | 174,61 | 198. |
| F # 3 / G b 3 | 185,00 | 186. |
| G 3 | 196,00 | 176. |
| G # 3 / A b 3 | 207,65 | 166. |
| А 3 | 220.00 | 157. |
| A # 3 / B b 3 | 233,08 | 148. |
| В 3 | 246,94 | 140. |
| К 4 | 261,63 | 132. |
| C # 4 / D b 4 | 277,18 | 124. |
| Д 4 | 293.66 | 117. |
| D # 4 / E b 4 | 311,13 | 111. |
| E 4 | 329,63 | 105. |
| Факс 4 | 349,23 | 98,8 |
| F # 4 / G b 4 | 369,99 | 93,2 |
| г 4 | 392.00 | 88,0 |
| G # 4 / A b 4 | 415,30 | 83,1 |
| А 4 | 440,00 | 78,4 |
| A # 4 / B b 4 | 466,16 | 74,0 |
| В 4 | 493,88 | 69,9 |
| К 5 | 523.25 | 65,9 |
| C # 5 / D b 5 | 554,37 | 62,2 |
| Д 5 | 587,33 | 58,7 |
| D # 5 / E b 5 | 622,25 | 55,4 |
| E 5 | 659,26 | 52,3 |
| Факс 5 | 698.46 | 49,4 |
| F # 5 / G b 5 | 739,99 | 46,6 |
| г 5 | 783,99 | 44,0 |
| G # 5 / A b 5 | 830,61 | 41,5 |
| А 5 | 880,00 | 39,2 |
| A # 5 / B b 5 | 932.33 | 37,0 |
| В 5 | 987,77 | 34,9 |
| К 6 | 1046,50 | 33,0 |
| C # 6 / D b 6 | 1108,73 | 31,1 |
| Д 6 | 1174,66 | 29,4 |
| D # 6 / E b 6 | 1244.51 | 27,7 |
| E 6 | 1318,51 | 26,2 |
| Факс 6 | 1396.91 | 24,7 |
| F # 6 / G b 6 | 1479,98 | 23,3 |
| г 6 | 1567,98 | 22,0 |
| G # 6 / A b 6 | 1661.22 | 20,8 |
| А 6 | 1760,00 | 19,6 |
| A # 6 / B b 6 | 1864,66 | 18,5 |
| В 6 | 1975,53 | 17,5 |
| К 7 | 2093,00 | 16,5 |
| C # 7 / D b 7 | 2217.46 | 15,6 |
| Д 7 | 2349,32 | 14,7 |
| D # 7 / E b 7 | 2489.02 | 13,9 |
| E 7 | 2637.02 | 13,1 |
| Факс 7 | 2793,83 | 12,3 |
| F # 7 / G b 7 | 2959.96 | 11,7 |
| G 7 | 3135,96 | 11,0 |
| G # 7 / A b 7 | 3322,44 | 10,4 |
| А 7 | 3520,00 | 9,8 |
| A # 7 / B b 7 | 3729,31 | 9,3 |
| В 7 | 3951.07 | 8,7 |
| К 8 | 4186.01 | 8,2 |
| C # 8 / D b 8 | 4434,92 | 7,8 |
| Д 8 | 4698,64 | 7,3 |
| D # 8 / E b 8 | 4978,03 | 6,9 |
Как работает музыка
Предупреждение: Javascript отключен в этом браузере.Хотя этот веб-сайт будет правильно работать без Javascript, вам будет менее удобно использовать его.
Мы рекомендуем вам включить Javascript в этом браузере или использовать другой браузер, если он у вас есть.
Хроматическая гамма может начинаться с любой ноты, но всегда будет содержать одни и те же ноты (потому что она содержит все ноты). Таким образом, на практике существует только одна хроматическая шкала.
В таблице ниже показаны частоты двенадцати нот между нотой А на 440 Гц и нотой А на октаву выше.
Высокие ноты имеют большие частотные шаги (в герцах) между ними, но каждый шаг приводит к одинаковому изменению воспринимаемой нами разницы в высоте тона (один полутон).
Несмотря на то, что в октаве двенадцать нот, только первые семь букв алфавита используются для их названия (от A до G). Мы рассмотрим причину этого позже.
Остальные пять нот хроматической гаммы получают название, помещая символ (#) после буквы ноты, чтобы сделать ее на один полутон выше, или помещая плоский символ (b) после буквы ноты, чтобы сделать ее на один полутон ниже.
Часто для этих пяти других нот есть два варианта названия. Например, нота A ♭ в таблице выше также может называться G #. Иногда, как мы увидим позже, существует определенное правило, для которого имя более подходящее.
Создание музыки с помощью Songtrix
Воплотите эти музыкальные концепции в жизнь с помощью бесплатного Songtrix Bronze Edition , когда вы создаете песни из аккордов и гаммы .Затем опубликуйте и поделитесь своими идеями с другими музыкантами, которых вы встретите в сети ChordWizard.
Есть вопросы? Присоединяйтесь к сети ChordWizard Network и размещайте их на форуме теории музыки, чтобы получить ответы и обсудить интересующие вас темы.
Больше информации Скачать
Какие частоты у музыкальных нот, таких как G, в килогерцах?
Спрашивает: Неизвестный Отправитель
Ответ
Существует два принятых стандарта высоты звука, так называемый американский стандарт высоты звука, который принимает Ля в четвертой фортепианной октаве (A4) должна иметь частоту 440 Гц, а более старая международная высота звука стандарт, который требует A4, чтобы иметь частоту 435 Гц.Оба эти стандарта шага определяют так называемые «равномерно темперированные хроматические гаммы». Математически это означает, что каждый последующий высота звука связана с предыдущей высотой тона с коэффициентом корня двенадцатой степени из 2. То есть отношение между частотами любых двух последовательных высот в любом стандарте — 1.05946309436. Там — это третья шкала Scientific или Just Scale, основанная на C4 с частотой 256 Гц, но это не используется в музыкальных целях.В октаве двенадцать полутонов (черная и белая клавиши на фортепиано) или шагов.Поскольку высота тона (частота) каждого последующего шага связана с предыдущим шагом корнем двенадцатой степени из 2, двенадцатая ступень выше заданной высоты звука ровно в два раза превышает начальную высоту звука. То есть октава точно соответствует удвоению высоты тона.
Частота промежуточных нот или высоты тона может быть найдена простым умножением (делением) учитывая начальную высоту звука на столько раз корня двенадцатой степени из 2, сколько шагов до (вниз) желаемый шаг.10 = 440 x 1,78179743628 = 783,99 Гц (приблизительно). Аналогичным образом, в международном стандарте G5 имеет частоту 775,08 Гц (приблизительно). G # 5 — это еще один множитель 12-го корня из 2 выше этих значений, или 830,61 и 821,17 Гц, соответственно. Обратите внимание, когда подсчитывая шаги, что есть один полутон (шаг) между B и C, и E и F.
Эти тональные шкалы называются «равномерно темперированными» или «хорошо темперированными». Это относится к
компромисс, заключенный в использовании корня 12-й степени из 2 в качестве фактора, разделяющего каждую последующую высоту звука.7 =
1.49830707688, что немного меньше 1,5, необходимых для идеальной пятой части. Это небольшое
уменьшение (выравнивание) частоты называется «отпуском». Это необходимо по приборам
например, пианино, на котором можно играть в любой тональности, потому что невозможно настроить все 3, 5,
и т. д. с их точным соотношением (например, 1,5 для пятых) и одновременно имеют, например, все
октавы выходят точно в соотношении 2,0.
Ответил: Уоррен Дэвис, доктор философии.D., президент, Davis Associates, Inc., Ньютон, Массачусетс, США
Ответ на эти вопросы легко определяется математически, но немного предыстории. помочь учащемуся использовать математические отношения с уверенностью и пониманием.
Клавиатура фортепиано настраивается в октавах. Каждая октава состоит из тринадцати нот, из них тринадцатая — также начало следующей октавы. Начиная с A октава составляет A, A #, B, C, C #, D, D #, E, F, F #, G, G #, и снова A.Интервал между каждыми двумя последовательными нотами называется полушагом. Следовательно, есть 12 интервалов полутона, образующих так называемую октаву.
Во-первых, каждая октава вверх или вниз представляет удвоение частоты. Например, буква A выше средний C на фортепиано установлен на стандартное значение 440 Гц, поэтому для A на октаву выше частота 880 Гц.
А теперь подробности. Полушаг — это наименьший интервал, признанный в западной музыкальной теории.Кроме того, частоты музыкальных нот на стандартном пианино теперь устанавливаются в соответствии со стандартом. метод, называемый «равномерный настрой».
Примечания: Системы настройки не могут быть здесь подробно описаны. Короче говоря, есть компромисс в используя одинаковый темперамент в том смысле, что все гармонии немного несовершенны, но этот метод дает подавляющее преимущество перед своими предшественниками в том, что музыка может быть написанным в любом ключе с равным гармоничное качество для каждого.
Бах популяризировал уравновешенный темперамент и продемонстрировал его эффективность в серии своих произведений. части во всех тональностях, известные как «Хорошо темперированный клавир». Равномерно темперированный метод настройки разработка увлекательна с исторической точки зрения (как с научной, так и с музыкальной). В другие методы настройки и вся природа гармонии, основанные на обертонах фундаментальных частоты, при этом частоты обертона определяются как кратные основным частотам, заслуживает дальнейшего внимания заинтересованного читателя.
Вернуться к нашей исходной истории. В этой равнотемперной системе настройки частоты нот на клавиатуре связаны довольно простой математической зависимостью, включающей количество клавиш (полутона) между нотами.
Для определения взаимосвязи между известной частотой ноты и неизвестной частотой
(хотел бы быть известным) другого примечания, умножьте известную частоту на 2 в степени
(Количество полушагов / 12). (# ofhalf-Step) положительно, если нужно двигаться ВВЕРХ по частоте, чтобы достичь
обратите внимание с неизвестной частотой и отрицательным, если ВНИЗ.(-12/12) равно 0,5.
Ответил: Тайлер Грубер, доктор философии, адъюнкт-профессор физики, Louisiana Tech U.
Фурье, часть 2.2
Фурье, часть 2.2Аппроксимации Фурье и музыка
Часть 2: Музыкальные ноты
2.2 Высота и наименование нот
Когда мы слышим, как музыкальный инструмент издает ноту, мы имеем общее представление о ее высоте. Например, мы знаем, что пикколо звучит относительно высокочастотными нотами, а туба — относительно низкочастотными нотами. Названия, связанные с этими нотами — «A», «C # » и т. Д. — определяются исключительно высотой тона.
Наиболее широко распространенное соглашение об именах для нот, действующее с середины 19 века, использует следующий метод для присвоения имен нот конкретным частотам.Частоте 440 герц назначена нота А. Это нота, которую вы слышите из гобоя, когда оркестр настраивается. Вы произносите эту ноту на фортепиано, ударяя по 40-й клавише справа, считая как черные, так и белые клавиши. В диапазоне от 440 до 880 Гц имеется тринадцать именованных нот, считая обе граничные частоты. Эти примечания: A, A # , B, C, C # , D, D # , E, F, F # , G, G # , A — где символ # читайте «острый».»Соотношение частот любых двух следующих друг за другом нот в этом списке примерно одинаково, т.е. частоты образуют геометрическую последовательность.
Таким образом, если вы начнете с клавиши пианино с частотой 440 Гц (40-я клавиша справа) и ударьте по ней вместе со следующими 12 клавишами справа по порядку, вы сыграете эти ноты. Первая и последняя ноты в этой последовательности имеют одно и то же имя — «А». Тот же самый образец наименования применяется к нотам между 880 и 1760 герцами, и так далее вверх и вниз по диапазону слышимых частот.
Таким образом, для любых двух последовательных нот с одним и тем же именем частота более высокой ноты будет вдвое больше частоты более низкой ноты. Говорят, что он на октавы на выше оригинала. (Когда вы поете гамму до-ре-ми, до в начале и до в конце разнесены на одну октаву.) У полноразмерного фортепиано 88 клавиш и, следовательно, он охватывает чуть более 7 октав. Самая высокая нота А на фортепиано (третья белая клавиша справа) имеет частоту 3520 герц.
- Найдите соотношение частот двух последовательных нот, то есть двух соседних клавиш на клавиатуре фортепиано.
- Найдите частоту ноты C над средней A (440 Гц).
- Найдите частоту первой ноты на левом конце фортепианной клавиатуры. Как называется эта записка?
Соотношения частот и восприятие высоты звука — Понимание звука
Клавиатура фортепиано
На фортепиано клавиши расположены в порядке высоты тона, при этом самые низкие частоты находятся в крайнем левом углу клавиатуры.Внимательно посмотрите на клавиатуру, и вы заметите повторяющийся узор из двенадцати клавиш. Неудивительно, что музыкальные ноты помечаются с помощью цикла. Белые клавиши пианино обозначены буквами от A до G. Чтобы различать разные A, нижняя A на пианино обозначена A0, следующая нижняя A обозначена A1 и так далее. Схема небольшой части фортепианной клавиатуры ниже иллюстрирует эту идею.
Названия нот на клавиатуре фортепиано.Чтобы услышать, как устроена клавиатура пианино, поиграйте с этой пятиоктавной онлайн-клавиатурой или этой маленькой флэш-клавиатурой с помеченными клавишами.
октава
Расстояния вдоль клавиатуры фортепиано называются музыкальных интервалов — для краткости интервалов. Интервал от одного A до следующего A (или от одного D до следующего D) называется октавой . Вы, наверное, слышали октаву раньше — и «Где-то над радугой», и «Жареные каштаны на открытом огне» начинаются с октавного скачка. Октава — действительно важный интервал по двум причинам. Во-первых, октава особенно удобна для слуха — две ноты, разнесенные на октаву, бывает трудно различить, особенно когда играют вместе.Во-вторых, октава соответствует коэффициенту два по частоте. Нота, на которую настраиваются оркестры (A4), имеет основную частоту 440 Гц, иногда ее называют A440. Нота на октаву выше (A5) имеет основную частоту 880 Гц. Нота на октаву ниже (A3) имеет основную частоту 220 Гц.
Соотношения частот и восприятие высоты звука
Октава раскрывает кое-что важное о музыке и восприятии высоты тона: человеческое восприятие «расстояния между двумя высотами» зависит от соотношения частот двух нот — чем больше соотношение , тем дальше кажутся звуки.Две частоты, разделенные на два раза, всегда звучат на октаву друг от друга, независимо от того, являются ли эти две частоты 500 Гц и 1000 Гц или 10 000 Гц и 20 000 Гц. Разница частот почти ничего не говорит о воспринимаемой разнице в высоте тона.
Перестань думать
- Какова частота ноты на две октавы выше ноты с частотой 300 Гц?
- Одна нота на 200 Гц выше другой. Какой музыкальный интервал между нотами?
- Какой музыкальный интервал больше: от 1000 Гц до 2000 Гц или от 2000 Гц до 3000 Гц?
Частоты и клавиатура
На приведенной ниже диаграмме показаны частоты каждой ноты на клавиатуре фортепиано.По мере того, как вы идете направо, штанги становятся выше. Это неудивительно — высокие ноты находятся на правом конце фортепиано. Что может быть удивительно, так это то, что график — это не линия. Это потому, что музыкальные интервалы основаны на умножении, а не на сложении. При перемещении одной клавиши пианино вправо частота не увеличивается на определенное количество герц. На самой низкой ноте фортепиано перемещение одной клавиши вправо увеличивает частоту менее чем на 2 Гц. На верхнем конце фортепиано перемещение по одной клавише увеличивает частоту более чем на 200 Гц.То, что осталось прежним, — это увеличение на процентов — когда вы перемещаете одну клавишу вправо, новая частота будет примерно на 6 процентов выше, чем предыдущая нота. Другими словами, соотношение частот одной клавиши пианино к следующей составляет около 1,06.
Частоты нот на фортепиано.Если вы действительно хорошо разбираетесь в математике, вы, вероятно, заметите, что математика для фортепиано идентична математике для сложных процентов при 6%! Это потому, что отношение между восприятием высоты звука и частотой является логарифмическим.Если вы нанесете на график логарифмов частот над каждой из нот вместо фактических частот, картина фортепиано станет линейной:
Логарифмы частот нот на фортепиано.Теперь перемещение одной клавиши по клавиатуре всегда увеличивает общий логарифм частоты на одну и ту же величину — примерно на 0,025. Суть в том, что люди воспринимают высоту звука в терминах логарифма частоты, а не самой частоты.
Логарифмические шкалы для частотных графиков
Когда вы строите график, вы выбираете, как расположить числа вдоль оси.Например, когда вы строите график БПФ, каждый сантиметр по оси x может представлять определенную частоту (скажем, 100 Гц). В результате частоты равномерно распределены по оси абсцисс. Это называется линейным шагом или линейным масштабированием . Если вы используете линейный интервал для БПФ, вы столкнетесь с проблемой — каждая октава занимает все больше и больше места на графике по мере увеличения частоты.
Одно из решений — расположить числа частот на графике так, чтобы каждая октавы занимала одинаковое пространство вдоль оси.Это называется логарифмическим масштабированием (также называется логарифмической шкалой и логарифмическим интервалом ).
Два графика ниже показывают разницу между линейным и логарифмическим масштабированием. При линейном интервале (нижняя панель на рисунке ниже) каждые 1000 Гц занимают одинаковое пространство на оси. Каждая октава занимает все больше и больше места по мере увеличения частоты — обратите внимание, что октава от 10 000 Гц до 20 000 Гц занимает в десять раз больше графического пространства, чем октава от 1 000 Гц до 2 000 Гц!
Расстояние между бревнами (показано на верхней панели) более точно соответствует тому, что мы слышим.Каждая октава занимает одинаковое количество места на графике. Теперь частоты от 100 до 200 Гц занимают столько же места, что и частоты от 1000 до 2000 Гц. Горизонтальные расстояния на лог-графике показывают музыкальные интервалы. Например, вы можете легко увидеть, что музыкальные интервалы между одним обертоном и другим становятся меньше на более высоких частотах.
Два БПФ одного и того же спектра: верхний график имеет логарифмический интервал на оси частот, нижний график имеет линейный интервал.Перестань думать ответы
- Две октавы выше 300 Гц составляют 1200 Гц.Каждая октава выше удваивает частоту — одна октава выше 300 Гц равна 600 Гц; на октаву выше — 1200 Гц.
- Два тона, различающиеся на 200 Гц, могут составить практически любой музыкальный интервал. От 200 Гц до 400 Гц — это ровно октава — соотношение частот точно равно двум, но 2000 Гц и 2200 — намного меньше, чем разница в октаве — соотношение намного меньше двух.
- Интервал от 1000 Гц до 2000 Гц больше. Сравните соотношения частот: (2000 Гц) / (1000 Гц) = 2 и (3000 Гц) / (2000 Гц) = 1.5. Интервал между 1 кГц и 2 кГц составляет одну октаву; интервал между 2 кГц и 3 кГц меньше октавы.
Изображение предоставлено
- Названия нот на клавиатуре фортепиано. Адаптировано из текста Schmidt-Jones Introduction to Music Theory на OpenStax)
- Частоты нот на фортепиано. Создано Дэвидом Эбботтом.
- Логарифмы частот нот фортепиано. Создано Дэвидом Эбботтом
- Два БПФ одного и того же спектра: верхний график имеет логарифмический интервал на оси частот, нижний график имеет линейный интервал.Создано Дэвидом Эбботтом с использованием Audacity.
- Нота на октаву выше, чем конкретная нота, имеет дважды частота как рассматриваемая заметка. Эти две ноты смешаются
и хорошо звучат вместе. На рисунке 12.14 показаны два примечания, которые
на октаву друг от друга.
Но как ноты размещены между октавами? Пифагор, в
пятого века до нашей эры, отметил, что арфы издают приятные звуки,
длины их строк были пропорциональны маленьким целым числам.На рисунке 12.15 показаны ноты фортепианной клавиатуры и высокие частоты.
ключ, охватывающий октаву, начиная с середины C. Ноты C, E,
и G имеют частоты в соотношении 4: 5: 6. Когда в них играют
вместе, три ноты очень хорошо сочетаются и приятно
ухо; эти ноты образуют мажорное трезвучие или мажорный аккорд.
Частота среднего до 262 Гц. Это и требует приятного
тона мажорного трезвучия, затем определите частоты (или высоты тона)
E (262 Гц x (5/4) = 327.5ÊГц) и G (262 Гц x (6/4) =
393 Гц). C ‘, будучи на октаву выше средней C, имеет частоту
524 Гц. Ноты F, A, C ‘также образуют мажорное трезвучие (или мажорное трезвучие).
аккорд), который определяет частоту (или высоту тона) нот F
(524 Гц x (4/6) = 349 Гц) и A (524 Гц x (5/6) = 437 Гц). Так же,
ноты G, B и D ‘также образуют мажорное трезвучие (или мажорный аккорд
и это определяет частоту (или высоту тона) нот B (393 Гц
x (5/4) = 491 Гц) и D ‘(393 Гц x (6/4) = 589,5 Гц). Рисунок 12.16
перечисляет частоты всех белых нот пианино, если мы
Настройтесь на эти мажорные трезвучия, начав со средней C.Этот
называется диатонической гаммой в тональности C. Однако мы могли
начали с другой ноты. На рисунке 12.16 также перечислены
частоты всех белых нот пианино, если мы настроимся на эти
мажорные трезвучия, начинающиеся с D выше среднего C. Это называется
диатоническая гамма в тональности D. Видно, что некоторые частоты
такие же, но большинство из них несколько отличаются!
Это означает, что мы можем настроить пианино на диатоническую гамму в тональности C, но тогда это звучало бы забавно, если бы мы попытались написано в тональности Д.Основные трезвучия или аккорды, которые должны звучать приятно вместе больше не звучит хорошо. В течение восемнадцатого пианино и клавесины века — и все инструменты — были настроены к определенной тональности определенного музыкального произведения. Они бы необходимо перенастроить на другой ключ для исполнения другая пьеса написана в другом ключе.
Чтобы избежать лишнего труда и утомительности при перенастройке, схема из линейки с одинаковым темпом плавления была разработана модель . В том числе черные клавиши — диез и бемоль — на клавиатуре пианино, там это двенадцать нот, называемых полутонами, между C и C ‘.Мы требуем что частота C ‘вдвое больше частоты C и что отношение частот соседних полушаговых нот или клавиш одно и тоже. То есть соотношение частот соседних клавиш должен быть корнем двенадцатой степени из 2 (то есть (1.05946) 12 = 2). Что есть, если частота каждого ключа в 1,06 раза больше частоты соседний ключ, к тому времени, когда вы перейдете от середины C через двенадцать клавиш и достигают C ‘на октаву выше, частота of C ‘будет ровно в 2 раза чаще средней C.Фигура 12.16 также перечислены частоты нот этого одинакового закаленная шкала. Это компромисс, так что ноты и аккорды все клавиши одинаково хорошо (или плохо) звучат при игре на этой шкале.


 35
35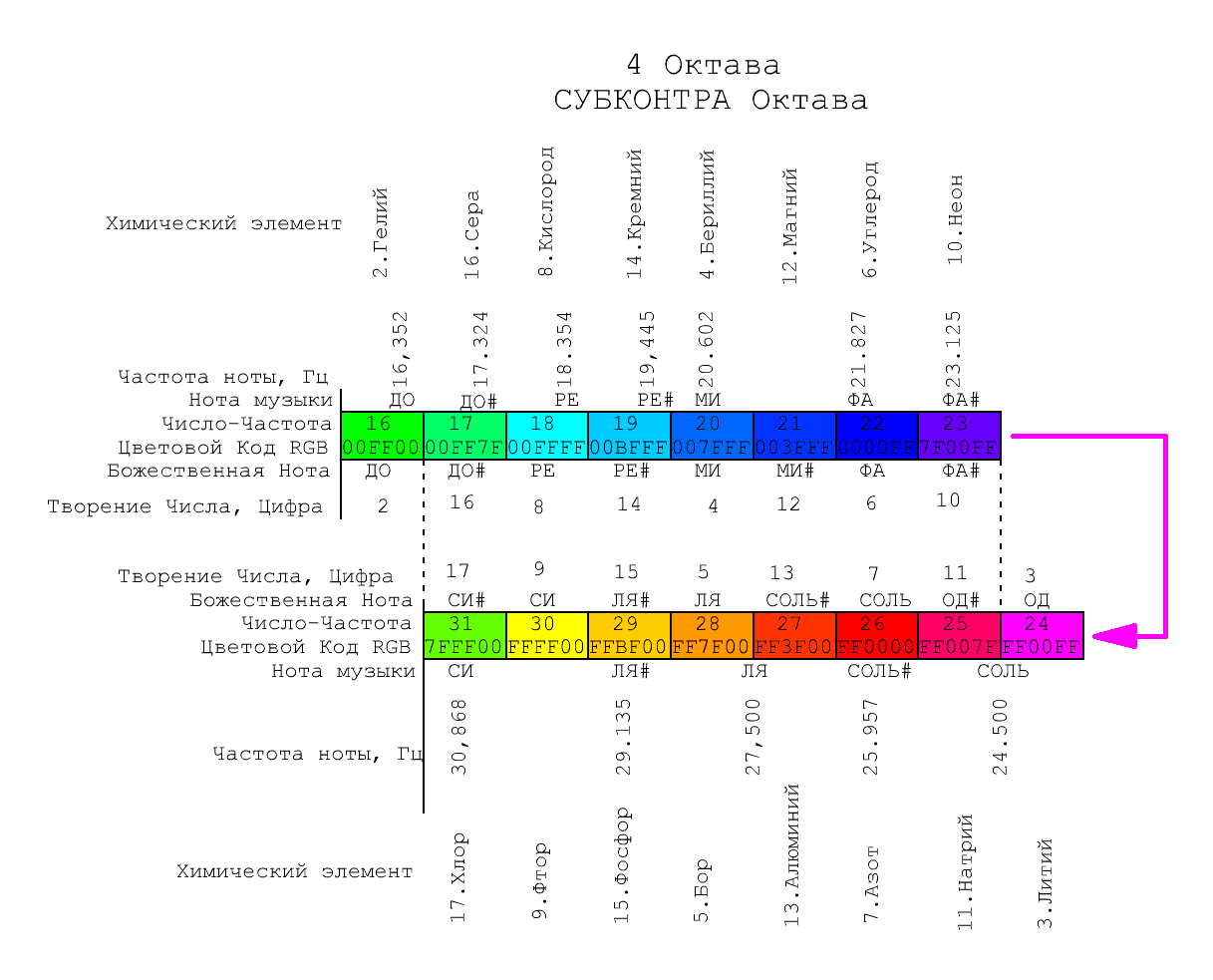 6
6 Обычно величина скорости звука принимается равной 343 м/м для температуры 20oC.
Обычно величина скорости звука принимается равной 343 м/м для температуры 20oC.