Подкова в геометрии что значит: что значит в геометрии подкова в бок «с»

Содержание

что значит в геометрии подкова в бок «с»

ДАЮ 64 БАЛА!!! ЗА » МНЕ ЛЕНЬ» БАЛЫ НЕ ДАЮ!!! ФОТО С САМИМ ЗАДАНИЕМ ПРИКРЕПЛЕНО! ТАМ ГДЕ «?» НУЖНО ВСТАВИТЬ БУКВЫ ЛИБО ЧИСЛА!!! ПОДХОДИТ ОТВЕТ И НА РУС … СКОМ, И НА УКРАИНСКОМ! Периметр трикутника ABC дорівнює 6 см, периметр трикутника DEF — 8 см. Доведи, що периметр шестикутника PKLMNR менший, ніж 7 см. 1. Розглянь трикутники PAK, KDL, LBM, MEN, NCR і RFP. Напиши для кожного з них нерівність трикутника для сторін, які також є сторонами шестикутника. PK < PA + ? KL < ?+? ?<?+? ?<?+? ?<?+? ?<?+? 2. Якщо додати праві та ліві сторони правильних нерівностей, отримаємо правильну нерівність. Яку з величин отримаємо в лівій стороні після додавання? 1. подвоєний периметр трикутника DEF 2. подвоєний периметр трикутника ABC 3. периметр трикутника DEF 4. периметр шестикутника PKLMNR 5. подвоєний периметр шестикутника PKLMNR периметр трикутника ABC 3. Якщо до обох сторін правильної нерівності додати одну й ту саму величину, отримаємо правильну нерівність. Додай до обох сторін отриманої в попередньому кроці правильної нерівності PK+KL+LM+MN+NR+RP. Які з величин отримаємо в лівій стороні після додавання? 1. подвоєний периметр трикутника DEF 2. подвоєний периметр шестикутника PKLMNR 3. периметр трикутника ABC 4. периметр трикутника DEF 5. подвоєний периметр трикутника ABC 6. периметр шестикутника PKLMNR 4. Які з величин отримаємо в правій стороні після додавання? 1. подвоєний периметр трикутника DEF 2. периметр трикутника ABC 3. подвоєний периметр трикутника ABC 4. подвоєний периметр шестикутника PKLMNR 5. периметр шестикутника PKLMNR 6. периметр трикутника DEF 5. Чому дорівнює права сторона отриманої нерівності, якщо використовувати дані числові значення? Відповідь: ? 6. Що необхідно зробити з обома сторонами отриманої нерівності, аби довести, що периметр шестикутника PKLMNR менший, ніж 7 см? 1. поділити на 2 2. додати 2 3. відняти 2 4. помножити на 2 5. це неможливо довести

heeeeeeeeeeeelp 9 раз больше другого 9!!!!

На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC. Во сколько раз сторона AB больше высоты, проведённой к этой стороне?

ДАЮ 100 БАЛОВ!!! ЗА » МНЕ ЛЕНЬ» БАЛЫ НЕ ДАЮ!!! ФОТО С САМИМ ЗАДАНИЕМ ПРИКРЕПЛЕНО! ТАМ ГДЕ «?» НУЖНО ВСТАВИТЬ БУКВЫ ЛИБО ЧИСЛА!!! Периметр трикутника A … BC дорівнює 6 см, периметр трикутника DEF — 8 см. Доведи, що периметр шестикутника PKLMNR менший, ніж 7 см. 1. Розглянь трикутники PAK, KDL, LBM, MEN, NCR і RFP. Напиши для кожного з них нерівність трикутника для сторін, які також є сторонами шестикутника. PK < PA + ? KL < ?+? ?<?+? ?<?+? ?<?+? ?<?+? 2. Якщо додати праві та ліві сторони правильних нерівностей, отримаємо правильну нерівність. Яку з величин отримаємо в лівій стороні після додавання? 1. подвоєний периметр трикутника DEF 2. подвоєний периметр трикутника ABC 3. периметр трикутника DEF 4. периметр шестикутника PKLMNR 5. подвоєний периметр шестикутника PKLMNR периметр трикутника ABC 3. Якщо до обох сторін правильної нерівності додати одну й ту саму величину, отримаємо правильну нерівність. Додай до обох сторін отриманої в попередньому кроці правильної нерівності PK+KL+LM+MN+NR+RP. Які з величин отримаємо в лівій стороні після додавання? 1. подвоєний периметр трикутника DEF 2. подвоєний периметр шестикутника PKLMNR 3. периметр трикутника ABC 4. периметр трикутника DEF 5. подвоєний периметр трикутника ABC 6. периметр шестикутника PKLMNR 4. Які з величин отримаємо в правій стороні після додавання? 1. подвоєний периметр трикутника DEF 2. периметр трикутника ABC 3. подвоєний периметр трикутника ABC 4. подвоєний периметр шестикутника PKLMNR 5. периметр шестикутника PKLMNR 6. периметр трикутника DEF 5. Чому дорівнює права сторона отриманої нерівності, якщо використовувати дані числові значення? Відповідь: ? 6. Що необхідно зробити з обома сторонами отриманої нерівності, аби довести, що периметр шестикутника PKLMNR менший, ніж 7 см? 1. поділити на 2 2. додати 2 3. відняти 2 4. помножити на 2 5. це неможливо довести

9 класс. Легкие 35 баллов. Помогите пожалуйста , очень срочно.

В треугольнике OAB угол B равен 90 градусов AB=6, sin O=0,3. Найдите OB

Помогите, пожалуйста. Прям с решением каждая задача

Найти все углы дано А-38 С-90 И-?

Помогите пожалуйста. Прям с решением каждая задачка

Дано рівнобедрений прямокутний трикутник. Доведіть, що існує переміщення, яке відображає катет на другий катет. Чи існує переміщення, яке відображає к … атет на гіпотенузу?

Что означает символ подковы? Значение подковы на стенах дома и крышках гроба

Подкова

Металлическая изогнутая пластина по форме конского копыта вывешивается над дверью и окнами в качестве оберега, защищающего от напастей и привлекающего благодать. Подкова, как символ счастья и удачи , имеет не такие уж и глубокие корни. Появлению металлических подков, предназначенных для защиты копыт лошадей от повреждений и износа, предшествовали защитные плетенные из кожи, лыка или тростника «чулки» для лошадей. Металлические варианты подковы, вид которых знаком большинству современных людей, начали использоваться лишь только в Средние века.

Многие народы верят, что подкова способна защитить от нечистой силы, а также избежать неприятностей: у моряков прибитая к мачте подкова оберегала корабль от бурь, в жилых домах подкова над камином или печью защищала от проникновения злых духов.

Символизм подковы связан со своеобразной формой изделия, которая напоминает силуэт чаши и ассоциируется с женским Чревом. Вывешивая на стенах дома подкову, люди привлекают тем самым защиту богинь материнской женственности, которые оберегают не только семью и домашний очаг, но и весь род. Чашеобразная форма служит архетипичным вместилищем, пространство которого аккумулирует счастье. Именно поэтому чаще всего подкову размещают рожками вверх с тем, чтоб «счастье из дома не выходило».

Однако во многих европейских странах подкову рассматривают как оберег, приносящий благодать. Для того, чтоб усилить воздействие символа металлическую пластину вывешивают рожками вниз по типу арки или купола, который «осыпает благодать на головы хозяев дома».

Если же брать за основу металл, из которого изготавливались изделия, то люди издавна приписывали металлическим предметам свойства порабощать и контролировать надприродные силы. Одним из примеров может служить размещение подков при захоронении на крышках гроба ведьм, с тем, чтоб они не возрождались вновь.

Что означает?

1. Символ — кольцо Кладдаха?

КАК ОПРЕДЕЛИТЬ РАЗМЕР КОЛЬЦА? | www.zolpodkova.ru

Вы хотите заказать кольцо, но не знаете какой размер вам подойдет?

Все очень просто!

Размер пальца — это внутренний диаметр кольца в миллиметрах.

То есть, если после измерения у вас получился диаметр 18,5 мм.,

то размер кольца будет 18,5.

Разница между размерами составляет 0,5 мм., т.е. 17, 17,5, 18 и т.д.

Если у вас нет кольца — не расстраивайтесь!

Размер пальца можно вычислить, измерив его окружность ниткой или полоской бумаги.

Просто разделите получившуюся длину на число π (3,14) — округлите, это и будет диаметр окружности, и, соответственно, размер кольца.

Таблица размеров:

Длина окружности мм.	Диаметр мм.	Размер мм.
47,1	15	15
48,67	15,5	15,5
50,24	16	16
51,81	16,5	16,5
53,38	17	17
54,95	17,5	17,5
56,52	18	18
58,09	18,5	18,5
59,66	19	19
61,23	19,5	19,5
62,8	20	20
64,37	20,5	20,5
65,94	21	21
67,51	21,5	21,5
69,08	22	22
70,65	22,5	22,5
72,22	23	23
73,79	23,5	23,5
75,36	24	24
76,93	24,5	24,5
78,5	25	25

Важно помнить!

Кольцо обязательно должно проходить через сустав.

2. Размер пальца зависит от температуры и влажности воздуха. Лучше отложить замеры в знойную жару или сильный мороз.

3. Самое оптимальное время суток для замера — полдень: утром пальцы рук еще отекшие после сна, а вечером — уже отекли.

4. Также не стоит определять размер если у вас:

— менструация

— повышена температура тела

— после занятий спортом

— нервозное состояние.

P.S. Если сомневаетесь между двумя размерами — выбирайте больший!

Так как уменьшить размер кольца можно в любой ближайшей ювелирной мастерской,

а вот увеличить его, увы, не получится.

«Народные поверья. Оберег своими руками – «Подкова – символ счастья»

Мастер-класс по теме:

«Народные поверья. Оберег своими руками – «Подкова – символ счастья»

Разработано воспитателем высшей квалификационной категории Ивановой Т.А.

Задачи

расширить кругозор детей, познакомить с народными традициями и обычаями, обучить новым способам работы с пряжей и природным материалом, научить делать обереги;
развивать фантазию и творческие способности, самостоятельность, инициативу детей;
воспитывать уважения к народным традициям, воспитание познавательной потребности, интереса и активности, воспитание художественного и эстетического вкуса.

План–конспект занятия:

«Народные поверья. Оберег своими руками — подкова».

Цели :

Образовательная – расширить кругозор, познакомить с народными традициями и обычаями, обучить новым способам работы с пряжей и природным материалом, научить делать обереги;
Развивающая – развивать фантазию и творческие способности, самостоятельность, инициативу;
Воспитательная – воспитание уважения к народным традициям, воспитание познавательной потребности, интереса и активности, воспитание художественного и эстетического вкуса.

Тип занятия: мастер-класс
Продолжительность занятия: 45 минут.

Методы обучения: устное изложение материала, беседа, демонстрация образцов изделий, показ трудовых приемов.
Наглядно-демонстрационный материал: презентация и образцы оберегов.
Оборудование: ножницы, клей «Момент», пряжа, картон, сухоцветы, монетки, крупа, ягоды шиповника, семена тыквы и подсолнуха.

ХОД ЗАНЯТИЯ:

1. Организационный момент (2-3мин.)

Проверка присутствия учащихся. Проверка готовности учащихся к занятию.

2. Теоретическая часть: Сообщение нового материала.
(Изложение материала сопровождается показом оберегов)

Добрый день, гости дорогие,

Мы всех зовем

В наш уютный дом.

Проходите, не стесняйтесь,

Поудобнее располагайтесь.

А собрались мы для забавушки

Чтоб узнать, как жили наши бабушки,

Как делали обереги яркие,

Да самим смастерить подарки.

Сегодня на занятии, мы поговорим о народных поверьях, приметах, суевериях и славянских оберегах. Вы узнаете, как сделать оберег своими руками. Познакомитесь с основными правилами изготовления оберегов и их символами.

Уж так устроен человек, что даже у самых заядлых атеистов и нигилистов есть капелька суеверия. Обязательно постучим по дереву, сплюнем через левое плечо, а вернувшись, домой за забытой вещью, посмотримся в зеркало.

А, какие приметы вы знаете. (Ответы детей).

• Нечаянно рассыпать сахар — к хорошему, соль — к ссоре.

• Нельзя выбрасывать куски хлеба — к недостатку в доме; лучше скормить

птицам, животным.

• Не доел хлеб и взял другой кусочек незаметно для себя — кто-то из родных

вдалеке голоден.

• После ужина оставлять на столе недоеденные кусочки хлеба от своего

ломтя — оставляешь там свое счастье.

• Кто быстро ест, тот быстро и работает; ленивый ест медленно.

• Пересолила еду — влюбилась.

• Хранить в доме разбитую посуду — к несчастью.

• Не ешь с ножа — сердитым будешь.

• Дарить нож не следует — к ссоре; подаривший должен взять в обмен деньги,

хотя бы копейку.

• Не сиди на столе — бедным будешь.

• Ложка упала со стола – гость спешит.

• Не сметай со стола рукой — не будет достатка.

• Нельзя класть ключи на стол — не будут деньги водиться в доме.

• Не оставляй пустую бутылку на столе — будет безденежье.

• На себе или на ком-то нельзя ничего зашивать, пришивать — память, ум

зашьешь; если без этого невозможно обойтись, в рот взять ниточку и

держать до тех пор, пока шьют, — примета не сбудется.

• Зеркало разбилось — к беде, к разлуке.

• Наизнанку вещь надеть — битому быть.

• Не давай вечером взаймы ни денег, ни хлеба — не будет в доме ни того, ни

другого.

• Солнце село — ничего не выноси из дома; ни воду, ни мусор, ни деньги — к

разорению.

Ребята, оказывается, вы знаете очень много народных примет. Как вы думаете, почему и для чего люди издавна создавали приметы и верили в них? Верите ли вы в приметы?

Ответ: История возникновения народных примет и обычаев уходит в далекое прошлое, во времена языческих поверий. Люди пытались всячески защитить себя от могущественной и непознанной природы. Люди искали закономерности, анализировали собственные наблюдения. Таким образом, появились злые и добрые духи, плохие и хорошие приметы, начали появляться ритуалы и обычаи, призванные защитить и помочь выжить человеку в этом мире.

С незапамятных времен люди стремились защитить себя и свой дом от бед и несчастий. Для этого они делали обереги. Люди верили, что обереги охраняют их от болезни, «дурного сглаза», хищных зверей, стихийных бедствий, и разных напастей. Собираясь в дальний путь, человек брал с собой оберег, чтобы, вложенные в него, добро, вера и любовь согревали душу, напоминали об отчем доме, родной земле.

Самые сильные обереги – семейные реликвии. Это могут быть кольца, бусы, браслеты, игрушки, куклы, предметы одежды и предметы народного декоративно – прикладного творчества, передаваемые из поколения в поколение. Эти обереги обладают наибольшей силой, так как они защищают вашу семью уже давно, и их сила со временем только увеличивается.

Следующими по силе являются вещи, подаренные вам кем-то, кто вас искренне любит и желает вам всяческих благ. Таким может оказаться и любимый человек, и родственник, и кто-то из друзей.

Издавна люди беспокоились не только о том, как обезопасить себя, но и как уберечь свой дом от бед и напастей. На протяжении тысячелетий ни один дом на Руси не обходился без оберегов.

Люди верили, что в каждом доме живет домовой, которого надо задобрить, чтобы он не сердился и не вредил обитателям дома. Вот и мастерили своими руками самого домового и обереги для него обереги – домовушки: косу — домовушку, веночек, веничек, лапоть, хатку.

Обереги-домовушки очень добрые игрушки!
Они такие славные, красивые, нарядные,
Несут добро и радость в дом, здоровье и достаток!
Хранят семью и наш покой,
Отводят все невзгоды!

Сегодня мы поговорим об одном очень интересном обереге и даже сделаем его своими руками. Его название нам подскажут следующие строки:

Времени всадник мчался по кругу,

Жизнь затянув, как тугую подпругу,

Упала подкова с копыта коня…

На долгое счастье теперь у меня…

Случайное счастье свалилось к ногам,

Его ни за что, ни кому, не отдам,

Сверкнул, как первой весенней грозой,

В воронку времен унесло с головой.

В мире забвенья, где правит разлука,

Где люди, порой, не видят друг друга,

Нашли мы в пыли подкову на счастье,

значит — любовь нашли в одночасье.

Как это раньше я не понимала,

Нам ведь для счастья надо так мало…

Что бы по жизни с любовью идти,

Надо подкову в дороге найти.

История создания подковы

Первые приспособления сплетались в виде чулка или башмака из лыка, тростника, кожи, растительных волокон. Укреплялись над венчиком копыта под щёткой верёвками или ремнями. Эти башмаки были непрочны, укрепление их верёвками или ремнями вызывало дерматиты. Подошвенные поверхности копыт рабочего скота покрывали смолой.

Римляне употребляли для защиты подошвенной поверхности копыта металлические пластинки, большей частью овальной формы, с крючками, дужками, ушками или кольцами, для укрепления пластинки на копыте верёвкой или ремнём. Такие пластинки для лошадей назывались

гиппосандалиями, для мулов — мулосандалиями, для быков — бососандалиями.

В средние века научились крепить металлические подковы специальными гвоздями — ухналями.

В России ковочное дело начало развиваться на государственном уровне после Указа Петра I 1715 года: « В Москве и губерниях сыскать кузнецов добрых, взять во всякую губернию по два человека и велеть им учить кузнечному делу русских…». В 1732 году в селе Хорошево под Москвой была открыта первая в Европе коновальная школа.

Оберег «Подкова»

Это очень интересный и красивый оберег.

Издавна считается, что подкова – это талисман, который несет с собой счастье, удачу и богатство. Наши предки считали, что если найти подкову на дороге, то с этого времени ты станешь «баловнем» судьбы. Если настоящую подкову вам не найти, то купленная, подаренная или сделанная своими руками, она так же будет обладать сильнейшей энергетикой.

Мифы и легенды о подковах

Существует множество красивых сказок и легенд о подковах, приносящих удачу.

1. Наиболее известна легенда о святом Данстане. Он был искусным кузнецом и славился умением хорошо подковывать лошадей. Однажды к нему явился сам дьявол под личиной и попросил подковать его, выставив вперед ногу с нераздвоенным копытом. Но святой Данстан узнал лукавого. Он крепко привязал его к стене и принялся так грубо обрабатывать его ногу, что дьявол завопил и стал просить пощады. Однако святой Данстан не выпустил его до тех пор, пока тот не пообещал никогда не заходить в дом, где прибита подкова.

2. Считается, что впервые найденная подкова стала символом счастья в Древнем Египте. Коней, которых запрягали в повозки фараонов, подковывали золотыми подковами. Но материал подковы не делал крепче крепление – рано или поздно подковы оставались в пыли дороги. Разумеется, находка золотой подковы становилась счастьем.

3. В древней Руси были свои основания считать подкову символом грядущего счастья и оберегом от бед и нечистой силы. Дело в том, что все подковы выходили из-под молота кузнецов, всегда считавшихся борцами с нечистой силы. Кроме этого, подкова связана с конем, верным помощником крестьянина и воина.

4. Современные исследователи считают, что радость от найденной подковы объясняется тем, что в давние времена железо было большой редкостью, любое металлическое изделие считалось очень дорогим. Поэтому найти подкову, из которой можно было изготовить что-либо для дома – нож, скребок или просто гвоздь, действительно было счастьем.

Как сделать оберег

Оберегом могут стать самые разнообразные предметы. Силу свою обереги черпают первоначально от человека, их создающего: когда вы делаете их своим оберегом, вы должны вложить в них частичку свой энергии. Также силу свою они черпают в доверии к ним. При создании оберега думайте о чем-нибудь светлом и возвышенном. Вы должны полностью сконцентрироваться на процессе и мыслях о прекрасном, добром, вечном — ведь вы заряжаете свой оберег положительной энергией, которая будет потом вас охранять и помогать вам.

При работе требуется полное сосредоточение мыслей, направленных на цель изготовления берега и на его будущего владельца. Если не получается сосредоточиться, если в голову лезут посторонние мысли, вам стоит отложить изготовление оберега. Отдохните некоторое время, может быть, должно пройти несколько дней до того момента, когда вы сможете вновь приступить к изготовлению. Оберег сам даст знать, когда вы сможете его сделать. Вы просто почувствуете, что именно сейчас вы готовы вложить в него максимум позитивных эмоций и ваш оберег станет помощником и защитником.

Правила изготовления оберегов

Обереги не могут быть изготовлены для себя.

Никто не может заставить кого-либо изготовить для себя оберег. Обереги изготавливается только по доброй воле и от чистой души.
Самые сильные – те, которые изготавливаются для вас вашими кровными родственниками. Самые сильные обереги – супружеские кольца.
Нужно тщательно выбирать материал для изготовления оберегов. Их нужно выполнять только из природных материалов.
В процессе изготовления необходимо думать о том человеке, для которого делаете.

Важно запомнить:
При изготовлении оберегов не используются колющие и режущие предметы, так как будущая кукла должна стать другом и помощником человеку. Тряпочки и нитки для оберегов надо рвать, а не резать. Можно использовать целые куски изношенной одежды, насыщенной энергиями конкретного человека.
Кукла — оберег пропорциональна частям тела человека, что делает их образ гармоничным и завершенным. Ей не рисуют лица. Считается, если это сделать, то в куклу вселится чужой дух. А без лица, она просто передает через себя то, что вложил в неё человек, кусочек его души, добрых пожеланий, тепла.

Символика цвета в оберегах

Красный — успех в начинаниях, любви.
Оранжевый — сотрудничество.
Желтый — радость, символ здоровья и удачи.
Зеленый — практичность.

Голубой — изменения.
Синий — ответственность.
Фиолетовый — вера;
Бежево-коричневый — успех;
Пастельные тона — завершение;
Черный, белый, или жемчужно-серый — интуиция;
Красновато-коричневый, желтовато-коричневый — величие;
Коричневый с синим — счастливая дорога и ясное солнце.

Значение символов на оберегах

Злаки, бобовые — символ достатка, сытой жизни, благополучной в материальном аспекте.
Лапти символизируют домашний уют, семейное счастье.
Мак, зерна мака — символ исполнения желания.
Красный горький перец — мужское начало, символ мужского здоровья.
Шишка — символ трудолюбия и достижения успеха.
Лекарственные травы, ягоды шиповника — символ крепкого здоровья.
Лук оберегает семью от слез.
Ягоды рябины — символ женской молодости, красоты.
Бессмертник — символ долголетия.
Мешковина — изобилие.
Тыква, семена тыквы — символ плодородия, женского начала.
Хлеб — всему голова — согласие и достаток в доме.
Лавровый лист — слава, успех.
Плетение символизирует знакомства, дружбу с новыми интересными людьми.
Солнце, цветок подсолнуха — главный славянский оберег, славяне — дети солнца.
Семена подсолнуха — здоровье детей в доме.
Семя — зарождение новой жизни.
Кувшин — символ воды, полная чаша в доме.
Яйцо — продолжение рода.
Кукуруза — символ здоровья у детей, продолжения рода, сплоченности семьи, взаимопонимания.
Веник, направленный вниз, выметает ссоры из избы.
Веник, направленный вверх, — к деньгам.
Орех — символ умственной силы и здоровья.
Монетка — успех в делах.
Горшочки с кашей и молоком — достаток.
Фигурки мужчины и женщины, перевязанные ниточками, — любовь, неразрывность уз.
Петушок сахарный — чтобы в доме звучал радостный детский смех.
Чеснок и перец изгоняют нечистую силу.
Домашняя выпечка символизирует хлебосольность.
Сухоцветы — символизируют уют и красоту. Мешочек с можжевельником — символизируют чистоту мыслей.
Горох — мир и дружбу.

Мешок — символ богатства.
Полотно — счастье в доме.
Узелок оберегает от скандалов в доме.
Гнездо — продолжение рода.
Бублик, цепь — непрерывное кольцо, символ крепкой семьи.
Домик — символ семьи.
Мельница — перемелется — мука будет.
Крупа — мир, лад в доме, желая этого, молодых после венчания осыпали крупой.
Колосья, ягоды, дары природы — урожай в хозяйстве.
Коса, венок — символы бесконечности и непрерывности рода, возрастания благополучия.

Как правильно повесить оберег — подкову?

Вот что об этом было сказано в «Книге Потаённого Древа Жизни»:

«Чаша Светлая, где Счастие живёт, Добра Обитель, Знак Защиты.

Если хочешь дом спасти, вешай над дверью, если семью обрести – над очагом, если дитя – над кроватью супругов. Всякое дело во благо пойдет, ежели в себе зла не содержит. А коли кто вред замышляет – оградит от того Счастия Знак».

Подкова, направленная ветвями вверх, олицетворяет собой чашу, которая будет привлекать в дом богатство. Если же вы повесите подкову ветвями вниз, вся негативная энергия дома будет задерживаться на ней и стекать вниз, на землю. Обычно, таким образом подкову вешают для защиты дома от злых сил (порчи, сглаза).

В России с давних времён принято придерживаться такой традиции: внутри дома подкова вешается ветвями вверх, а снаружи, например, над крыльцом – ветвями вниз.

Как придать оберегу — подкове высшую Силу?

Очень важно помнить, что размещать подкову над дверью следует особым образом, а иначе она не сможет войти в свою полную Силу.

Во-первых, подкову нужно вешать только на один гвоздь и проследить, чтобы других вбитых гвоздей поблизости не было.

Во-вторых, обязательно прибивать подкову должны хозяин и хозяйка дома вместе. Если человек в доме живёт один, то одному ему и подкову прибивать.

В-третьих, перед тем как подкову повесить, должны хозяин с хозяйкой вместе за ветви подковы взяться и сказать следующие слова:

Как подкову на дверь прибиваем,

Так семью свою от всякой беды ограждаем,

Всё плохое за порогом оставляем,

Мир и лад в дом привлекаем!

Если вешает подкову один человек, то он должен перед этим за обе ветви руками взяться и сказать:

Как подкову на дверь прибиваю,

Так себя и дом от всякой беды ограждаю,

Всё плохое за порог выгоняю,

Любовь, радость в дом привлекаю!

Технологическая карта выполнения оберега – подкова

1. Вырезаете лекало нужного размера в форме подковы.

2. Накладываете лекало на картон, обводите карандашом, вырезаете.

3. Обвязываете заготовку оберега — подковы пряжей, применяя простые

узлы техники макраме. (Можно просто обвить заготовку пряжей).

4. Аккуратно приклеиваете горошинки и семечки.

5. Готовую подкову можно покрыть лаком.

Техника обвязки оберега – подкова узлами макраме

Для создания оберега применяем простые узлы техники макраме.

Складываем бечевку пополам, кладем петлей вверх под центр картонной подковы. Перегибаем петлю вперед на подкову, затем протягиваем два конца в петлю. Затягиваем петлю, потянув оба конца вниз.

Теперь откладываем один конец в сторону, а вторым продолжаем плетение. Рабочий конец бечевки кладем вперед на подкову, затем перегибаем за подкову и протягиваем в получившуюся петлю.

Далее этот же конец бечевки кладем уже за подкову, перегибаем вперед на подкову и протягиваем в петлю. Таким образом, чередуя два предыдущих узла, т.е. нитку заводим то через верх, то через низ, оплетаем один конец подковы. Затем продолжаем плетение другим концом бечевки, обрабатывая вторую сторону нашей картонной подковы. Свободные концы бечевки закрепляем горячим клеем. Из них в конце можно сделать петельку, на которую удобно будет вешать подкову. Теперь осталось только приклеить фасоль и горох. Наша подкова готова.

Пусть в доме счастье светиться всегда, пусть радость будет нескончаема и пусть поможет в этом вам, ваш милый сувенир!

Подкова, торговая сеть отзывы и оценка

Подкова — Ваша удача на дорогах!

=========Добро пожаловать!========
Мы уверены, что информация, которая размещена в нашей группе будет интересной и познавательной не только для опытных автомобилистов, но и для новичков.
==============================
Торговая Сеть Подкова — это сеть шинных центров, специализирующихся на продажах автошин, дисков и предоставлении услуг шиносервиса.

Цели и задачи нашей компании:
*Занять лидирующие позиции на шинном рынке в Алтайском крае.
*Лучший шиносервис автомобилей.
* Большой выбор качественных товаров по низким ценам.

Миссия: Мы работаем для обеспечения безопасности при передвижении автомобилей, что достигается продвижением качественных шин, дисков и услуг шиносервиса.

В наших магазинах Вы можете купить автошины и диски для всех видов транспорта, как для легковых авто, так и для грузовиков, известных марок: Aeolus,Aurora,Barum,Bridgestone,Cooper,Continental,
Dunlop,Falken,Firestone,Fulda,Gislaved,Goodride,GoodYear,Hankook,Kumho,Marshal,Michelin,
Nokian,Nordman,Sumo Firenza,Toyo,
Triangle,WestLake,Yokohama и другие.

Торговая Сеть Подкова существует на рынке с 2004 г и наша цель предоставить покупателю большой выбор качественных товаров по низким ценам.

Торговая Сеть Подкова за время своей работы установила тесные партнерские отношения с ведущими мировыми производителями и крупнейшими поставщиками автошин и дисков.

Мы уважаем наших клиентов и очень ценим их доверие. Наши взаимоотношения честны и открыты.

Мы никогда не останавливаемся на достигнутом и постоянно ведем работу по улучшению качества сервиса, расширению спектра товаров и услуг.

Мы стремимся сделать все возможное, чтобы Вы выбирали нашу компанию.
==============================
Наши адреса:
==============================
Барнаул, ул. Попова, 9, +7 (3852) 48-78-48

Барнаул, ул. Аносова, 1А, +7 (3852) 22-37-47

Барнаул,С.Власихинский, 67, +7 (3852) 55-50-75

Барнаул, ул. Покровская, 7 +7 (3852) 22-33-46
==============================
Мы работаем:
==============================
пн-пт с 8:00 до 20:00
сб-вс с 10:00 до 16:00
==============================
ПРИЧИНЫ ВЫБРАТЬ ТС ПОДКОВУ

Только качественные автошины и диски от ведущих мировых производителей.

Широкий ассортимент товаров, который удовлетворит самого взыскательного покупателя. Если нужного товара нет в наличии, есть возможность сделать заказ, который будет отработан в кратчайшие сроки.

Квалифицированное обслуживание. В любом из магазинов Вы сможете получить профессиональную консультацию. Для этого выскажите менеджеру свои пожелания при выборе шин/дисков, а также ожидания от дальнейшей эксплуатации.

Удобное расположение магазинов. Все ТСЦ расположены на удобных транспортных развязках в различных районах города.

Выгодные условия покупки. Накопительная система скидок на товары и услуги от 3 до 20%. Система дополнительных бонусов при покупке.

Опыт работы. Мы знаем свое дело. Наш опыт формирует профессионализм работы.

Форма подкова с пожеланиями на 62гр (мд) пластик

Пластиковая форма Подкова с пожеланиями рассчитана на 62 грамм мыла.

Пластиковая форма — важнейший элемент в мыловарении.

Она позволяет более точно выразить характер мыла, донести творческий замысел и воплотить любую задумку.

Формы на нашем сайте классифицируются по материалу, из которого они сделаны: пластиковые, силиконовые. Силикон в свою очередь делится на промышленные формы и формы 3D.

Пластиковые формы для мыла очень просты в использовании, вы просто наливаете мыльную основу в форму и ваше мыло готово.

Использовать ли отдушку и краситель — решать вам, даже без этого ваше мыло получится оригинальным и необычным именно благодаря пластиковой форме.

Ассортимент пластиковых форм для мыла очень велик, вы обязательно найдете что-то по душе.

Цветы, зверушки, сердечки, специальные формы к праздникам или простая геометрия. Все что вы захотите.

Пластиковая форма вас просто спасет, если у вас нет идеи как порадовать близких. Когда вы будете форму выбирать — у вас обязательно появится куча идей как именно будет выглядеть ваше мыло, так что про творческий кризис можете забыть навсегда. Навсегда или на несколько тысяч воплощенных идей точно. Ведь для одной формы вы можете придумать огромное количество сочетания цветов и ароматов и выглядеть ваше мыло будет всегда по-новому.

Иногда мыловары сталкиваются с проблемой — из пластиковой формы сложно извлечь готовое мыло. Именно поэтому многие выбирают силиконовые формы, ведь для того, чтобы достать мыло из силиконовой формы достаточно просто надавить в центр формы и мыло моментально окажется у вас в руках в целости и сохранности. С пластиком такой прием не проходит, т.к. пластиковая форма твердая.

Мыло из пластиковой формы пытаются достать ножом, портя рисунок и целостность мыла, иногда форму нагревают снизу, чтоб мыло подтаяло и его было легче достать, наконец ставят форму с мылом в морозилку, чтоб потом оно «выпало» из формы, но все эти способы не идеальны и зачастую наносят вред мылу.

Мы откроем вам секрет как избежать подобных трудностей.

Как же вытащить мыло из пластиковой формы?

Просто смажьте пластиковую форму маслом и только потом наливайте в нее расплавленную основу. Так вы без труда сможете достать готовое мыло.

Температурный диапазон работы с формой до + 70 градусов Цельсия. Этого вполне достаточно, чтоб совершать все необходимые манипуляции.

Главной особенностью форм является их многократное использование ,что говорит о высоком качестве изделия. Средняя толщина стенок пластика — 0,7-0,8мм — форма будет долго вам служить и радовать.

Регулярное пополнение каталога расширяет границы вашего творчества ,предоставляя тем самым возможность дарить заботу и радость своим близким и друзьям !Вы сможете подобрать форму к любому торжеству и ваш подарок несомненно оценят.

Выбирайте новые формы для мыловарения и продолжайте удивлять своих родных и друзей новыми шедеврами. А мы в свою очередь будем радовать вас новыми формами, как пластиковыми, так и силиконовыми.

Купить пластиковую форму для мыла недорого вы можете оформив заказ в нашем интернет магазине. Заказать пластиковую форму через интернет очень удобно — вы не ограничиваете себя временем, а это значит что ассортимент можно изучать хоть несколько дней. Если вам потребуется консультация — просто напишите нам: [email protected]

Дело за малым — осталось создать свое мыло!

Причины биения и вибрации автомобиля.

Сейчас мы разберём основные причины вибрации вашего автомобиля. Биение может проявлятся на разных скоростях и при торможении. Вибрация при движении и торможении автомобиля может быть связана с деформацией дисков, повреждением покрышек, нарушением балансировки колёс, состоянием тормозных дисков и колодок. Все наши клиенты в обязательном порядке получают консультацию о возможных рисках и последствиях неисправности тормозной системы и колёс автомобиля с заботой о безопасности. Рассмотрим основные виды неисправностей, причины и пути устранения вибрации.

Виды вибрации и биения

Вибрация всего кузова или руля автомобиля на определённых скоростях.
К примеру, вибрация в диапазоне скоростей от 90 до 100 км./ч является следствием разбалансировки колёс, нарушением формы колёсных дисков или отсутствием центровочных колец между колесом и ступицей автомобиля.

Вибрация всего кузова, педали тормоза или руля автомобиля при торможении.
Данный вид вибрации возникает в случае агрессивной езды с перегревом тормозных дисков или при резком перепаде температур (езда по лужам, автомойка). В данном случае потребуется проточка или замена тормозных дисков.

Раскачивание автомобиля или руля из стороны в сторону при движении на малых скоростях.
Это значит автолюбитель встретился с изломом протектора шины или значительной деформацией колесного диска.

Эти неисправности вызывают не только дискомфорт вождения и неравномерный износ шин, но и негативно влияют на подвеску, в частности на подшипники ступиц.

Неисправности

Деформация шин

В нашей практике встречались случаи заводского брака, особенно среди бюджетного сигмента шин. При сезонной замене шин рекомендуем менять их местами для равномерности износа. Если автомобиль долго стоит без движения, то это может привести к деформации резины. Важно правильно хранить шины. Мастера Подковы могут оценить ремонтопригодность шин и принять меры по восстановлению и выравниванию резины.

Деформация колесных дисков.

Причины нарушения геометрии диска — это наезд на поребрики, попадание в ямы или производственный брак. Чаще всего повреждается обод диска, а точнее его внутренняя часть.

Колесный крепеж

Очевидно, что крепеж должен быть подобран правильно и установлен с определенным моментом затяжки. Мы затягиваем болты динамометрическими ключами для избежания повреждений крепежа. Если крепеж затянут неравномерно или недостаточно, это можно почувствовать при разгоне.

Состояние тормозной системы

Деформация тормозных дисков может быть производственным браком или появиться в процессе эксплуатации, например, как неравномерная выработка. Биение в таких случаях ощущается при торможении, в том числе через педаль тормоза. Большинство современных автомобилей оборудованы антиблокировочными системами (ABS), антипробуксовочными (esp, asr, tcs, trs) и антизаносными системами. Алгоритм работы таких систем предусматривает исправное состояние тормозных дисков и колодок. Если тормозная система теряет эффективность, то работа этих жизненно важных систем становится грубой и не такой качественной.

Хаотическая подкова Смейла | plus.maths.org

30 ноября 1889 г. французский математик Анри Пуанкаре проблема. Он был награжден математической премией, предложенной no меньшим человеком, чем король Швеции Оскар II, за его работу над вопрос, который был надоедает математикам. Использование законов движения Ньютона и гравитации вы можете теоретически определить, как некоторые объекты (скажем, звезды, планеты и луны) должны двигаться из-за гравитационного притяжения, которое они воздействуют друг на друга. Если задействованы только два тела, ответ будет прямолинейны: они движутся по кривым, которые легко описать (эллипсы в случае планеты, вращающейся вокруг звезды). Проблема была в том, что произойдет, если вы бросите в смесь третий объект?

Стивен Смейл рассказывает о подкове на (несколько шумной) пресс-конференции на форуме Heidelberg Laureate Forum 2017. Щелкните здесь, чтобы посмотреть видео, в котором Смейл рассказывает о других аспектах своей работы и своей карьеры в целом.

В этом случае все становится непросто, но Пуанкаре проделал выдающуюся работу, пытаясь охарактеризовать движения. это может привести к системе с тремя телами. Проблема, с которой он столкнулся в ноябре 1889 года, заключалась в том, что работа содержала ошибку.Пуанкаре поступил правильно. Он признался и даже заплатил за копии своих работ, которые уже были напечатан. Он пересмотрел свою заявку на участие в конкурсе, все равно получил приз, и позже написал более подробно о том, что обнаружила ошибка ему. Это обнаружило существование хаоса.

Перенесемся в 1960 год и на пляжи Рио, где математик Стивен Смейл думал о проблеме, вдохновленной математикой радиоволн. Сложность проблемы беспокоила его, особенно с учетом того, что ранее он предполагал, что хаоса не существует.«Я сделал довольно плохие прогнозы», — говорит он. «[Норман] Левинсон из Массачусетского технологического института указал, что были эти старые статьи пары английских математиков [Мэри Картрайт и Дж. Л. Литтлвуд]. У них были интересные результаты, которые противоречили моим предсказаниям, и я хотел понять, что они сделали. Поэтому я поместил то, что я сделал, в очень геометрический контекст, чтобы я мог это понять ».

Результат теперь известен как Карта подковы Смейла . Он прекрасно передает, насколько хаотичным динамика может возникать в математике и непосредственно затрагивать суть проблемы, с которыми столкнулся Пуанкаре, когда думал о своем трехчастном проблема. «У Пуанкаре был большой беспорядок, и [подкова] наладила порядок в этом беспорядке».

Подкова

Посмотрите на область, показанную ниже, состоящую из квадрата с двумя закругленными концами, приклеенными вверху и внизу. Представьте, что вы поднимаете эту область, сжимаете ее в горизонтальном направлении и растягиваете в вертикальном направлении, так что она становится длинной и тонкой, а затем сгибаете ее вправо, чтобы образовалась подкова. Теперь поместите его обратно в исходную область, как показано.(Мы могли бы описать эту операцию с помощью математических формул, но замечательно то, что в этом нет необходимости — как вы увидите, суть динамики можно уловить концептуально.)

Подковообразная карта.

Поскольку подкова является частью исходной области, мы можем спросить, что с ней происходит, когда мы снова выполняем операцию сжатия, растяжения и сгибания. Это сжимает и растягивает подкову, а затем складывает ее в «четырехниточную» подкову, сидящую внутри простой подковы.

Применение карты подковы дважды к области D дает сложенную подкову.

Повторное выполнение операции превращает четырехниточную, сложенную один раз подкову в подкову, которая складывается дважды и имеет восемь нитей. Вы можете себе представить, как это продолжается, когда вы снова и снова выполняете операцию: вы получаете все больше змеиных подков с еще большим количеством прядей. Простая операция подковы приводит к довольно большим сложностям при повторном ее применении.

Подкова динамика

Операция дает динамическую систему : при многократном применении операции точки в регионе перемещаются. Точка в перемещается операцией (которую мы назовем) в другую точку в подкове, которая, в свою очередь, перемещается в точку в сложенной подкове при повторном применении, и так далее. Вы можете продолжать так до бесконечности, чтобы получить бесконечную последовательность очков. Эта последовательность называется прямой орбитой .

Точка x _-1

сопоставляется с точкой x ₀ под f , которая, в свою очередь, сопоставляется с x ₁.

Можно и наоборот. Вместо того, чтобы спрашивать, куда идет точка, вы можете спросить, откуда она взялась. Есть ли в этом смысл, когда вы обращаетесь к нему? Такой точки может и не быть, но если она есть, мы ее называем. Аналогично мы пишем для точки, которая идет под (если она существует), для точки, которая идет под (если она существует), и так далее.Последовательность называется обратной орбитой .

Все самое интересное происходит на Квадрате, образующем тело фигуры. Если он внутри, то нет никакой гарантии, что он тоже внутри — он может лежать в U-образном изгибе выше или в двух концах, торчащих из его нижнего края. Однако для некоторых точек точка действительно находится: если это так, то она находится в одной из двух вертикальных полос, в которых подкова пересекает квадрат.

Если x ₀ находится в S и x ₁ также находится в S , то x ₁ находится в одной из этих двух вертикальных полос.

Немного подумав, убедимся, что, следовательно, должно лежать в одной из двух горизонтальных полос, и. Когда вы применяете квадрат, эти горизонтальные полоски сжимаются по горизонтали и растягиваются по вертикали, а после того, как подкова была сформирована, ложитесь на наши две вертикальные полосы. Точки, которые находятся за пределами этих горизонтальных полос, сопоставляются с U-образным изгибом или двумя концами, выходящими из нижнего края.

Если x ₀ находится в S и x ₁ также находится в S , то x ₀ находится в одной из двух горизонтальных полос.

Что можно сказать о точках, в которых лежат целые передние и обратные орбиты ? Вы можете начать рисовать изображения того, где подковы с увеличивающимся количеством складок уходят или исходят по мере того, как вы наносите, или в обратном направлении, неоднократно. Через некоторое время у вас заболела голова, но оно того стоит, так как структура, которую вы обнаружите, очень интересна. Однако мы не будем делать этого здесь: есть более точный способ выяснить динамику набора точек, орбиты которых никогда не уходят.

Во-первых, напишите для этого набора точек, прямая и обратная орбиты которых не уходят. Учитывая точку, подумайте о любой другой точке на орбите, где может быть положительное или отрицательное значение. Точка — это следующая точка на орбите. И поскольку вся прямая и обратная орбита лежат внутри, мы это знаем, и оба лежат внутри. По тем же соображениям, что и выше, это означает, что он находится в одной из двух вертикальных полос, что, в свою очередь, означает, что находится в одной из двух горизонтальных полос или.Это верно для любой точки, другими словами, для любой точки на прямой и обратной орбитах. По мере того, как вы перемещаетесь по орбитам, точки подпрыгивают между и.

Переменная динамика

Это означает, что мы можем записать последовательность для каждого in. Сначала запишите if in и if in. Теперь посмотрите и запишите if in и if it is in. Затем посмотрите и запишите if in и if it is in. И так далее. Для каждой точки вашей прямой орбиты запишите a или a.Это дает вам бесконечную последовательность s и s.

Аналогичным образом мы можем записать последовательность для обратной орбиты, только теперь мы пишем ее справа налево. Первая запись (справа): если есть, а если есть. Вторая запись (справа): если есть, а если есть. И так далее. Это дает последовательность s и s, бесконечную слева.

Теперь склейте две последовательности вместе, поставив точку между последовательностями, чтобы разделить их. Например, последовательность

обозначает точку, в которой лежат вся прямая и обратная орбиты.

Точка p , последовательность которой целиком состоит из единиц.

Оказывается, соответствие между этими би-бесконечными последовательностями и точками, орбиты которых никогда не покидают квадрат, является точным. Вы можете доказать, что для каждой точки в существует уникальная би-бесконечная последовательность с точкой, а для каждой би-бесконечной последовательности с точкой существует уникальная точка. Если две точки расположены близко друг к другу, то их соответствующие последовательности соответствуют большому количеству мест слева и справа от точки, и наоборот — чем они ближе, тем больше мест совпадают.И, что лучше всего, применение карты к точке в соответствует смещению точки в ее последовательности вправо на одно место, а применение назад соответствует смещению ее вправо на одно место. Этот вид символической динамики часто используется в теории динамических систем и часто делает вещи удивительно прозрачными, как мы увидим дальше.

Об этой статье

Марианна Фрейбергер — редактор журнала Plus . Она поговорила со Стивеном Смейлом на форуме лауреатов Гейдельберга 2017.

Введение в математические символы для соединения и пересечения

Вопрос нашего читателя: « Есть два набора символов для« объединения »и« пересечения ». Один — и перевернутый ∩ , а другой набор — и ∧ . Какая связь между этими символами, которые мы иногда воспринимаем как «U» и «V» ? »

Итак, давайте вспомним о наших Мы и Против и их перевернутых товарищах в союзах и пересечениях, а также о логических функциях. с ∧ .

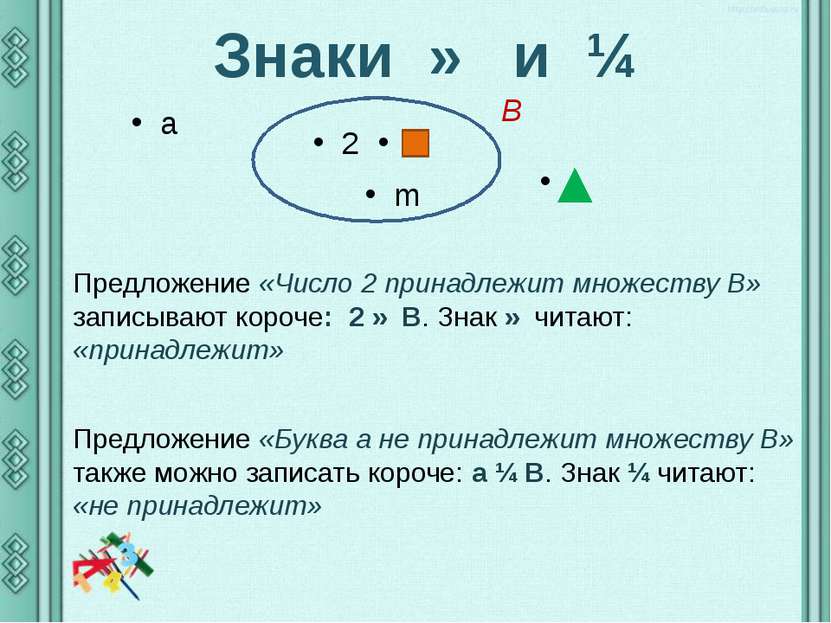
Символ «Объединение множеств» — « ∪ », а символ «пересечения множеств» — «∩».

Теория множеств для объединения и пересечения

Мы используем диаграммы Венна, чтобы показать объединения и пересечения. Изображение Майка ДеХаана

Подход, который наиболее тесно связан с этим вопросом, включает теорию множеств. Пусть A = {a, e, i, o, u, y} и B = {a, b, c, d, e, f}.

Объединение наборов «A» и «B» — это набор, содержащий уникальные элементы, обнаруженные либо в наборе «A», либо в наборе «B», либо в обоих.Другими словами, «Соберите все элементы вместе, но отбросьте дубликаты». A B = {a, b, c, d, e, f, i, o, u, y}.

Пересечение наборов «A» и «B» — это набор, содержащий уникальные элементы как из набора «A», так и из набора «B». Другими словами, чтобы создать пересечение, выберите только элементы, найденные в обоих исходных наборах, которые являются дубликатами, отброшенными операцией объединения. A∩B = {a, e}

Что касается исходного вопроса, с точки зрения теории множеств, слово «объединение» относится к символу « ∪ »; а слово «пересечение» относится к символу «».

Математические символы могут сбивать с толку! Изображение JRS

В вопросе нашего читателя мы также спрашивали о букве «V» и перевернутой букве «V», «Λ» или лямбде. Они используются в математической логике.

Пусть утверждение A = «Все люди — млекопитающие». Пусть B = «Все млекопитающие — люди». Пусть C = «Некоторые птицы могут летать при определенных условиях». И «A», и «C» — истинные утверждения, а «B» — ложь.

Пусть «X» и «Y» представляют любые, возможно, верные или ложные утверждения.

В математике логики утверждение «X и Y» или «XΛY» истинно тогда и только тогда, когда истинны и «X», и «Y».

Однако «X или Y» или «X ∨ Y» является ложным тогда и только тогда, когда оба «X» и «Y» ложны. «X ∨ Y» истинно, если истинно либо «X», либо «Y», что включает ситуацию, когда и «X», и «Y» истинны.

Из утверждений примера, «A B», «A ∨ C» и «B C» все верны. Однако «AΛB» и «BΛC» оба ложны. Только «AΛC» истинно, потому что каждое из утверждений «A» и «C» истинно.

Компьютеры для программирования с помощью «И» и «ИЛИ»

В зависимости от языка программирования «X и Y» могут быть представлены как «X && Y», а не «XΛY.3 = 2 * 2 * 2 = 8.

При письме на бумаге или когда текстовый редактор поддерживает надстрочный индекс, показатель степени отображается как надстрочный. См. Изображение выше.

Сводка математических символов для пересечения и объединения, и и или

В теории множеств пересечение и объединение обозначаются символами «» и « ∪ ». В математической логике операции «и» и «или» обозначаются буквами «Λ» и «V».

Объединение множеств «A ∪ B» можно рассматривать как объединение всех элементов «A», а также элементов «B»; но это будет , а не «и» (‘Λ’) математической логики.

Пересечение множеств «A∩B» еще меньше связано с логической операцией «или» (« ∨ »).

В других областях математики эти символы могут использоваться по-другому, но эти интерпретации имеют прямое отношение к вопросу читателя.

Ссылки :

Документация по Wolfram Mathematica. пересечение; Союз; И; Или же. (2012). По состоянию на 26 июля 2012 г.

Вуд, Алан. Символьный шрифт — альтернативы Unicode для греческих и специальных символов в HTML .(1997-2010). По состоянию на 26 июля 2012 г.

Майк ДеХаан применяет свою степень бакалавра математики в области компьютерных наук, годы программирования на языке Cobol и контроля качества (включая тестирование расчета процентов по кредитным картам) для исследования и представления математической теории для непрофессионала.

Здесь, в Decoded Science, Майк занимается математикой. Он изучает основы математической теории, раскрывает парадоксы, применяет вычисления к популярным фильмам и сообщает о математических новостях.
Майк начал профессионально писать в 2010 году как единственный владелец DeHaan Services.

Найди Майка в Google+

Общие математические символы и терминология

Математические символы и терминология могут сбивать с толку и препятствовать изучению и пониманию основ математики.

Эта страница дополняет наши страницы, посвященные навыкам счета, и предоставляет краткий глоссарий общих математических символов и терминологии с краткими определениями.

Мы что-то упускаем? Дайте нам знать.

Общие математические символы

+ сложение, плюс, положительное

Символ сложения + обычно используется для обозначения того, что два или более числа должны быть сложены вместе, например, 2 + 2.

Символ + также может использоваться для обозначения положительного числа, хотя он встречается реже, например, +2. На нашей странице о положительных и отрицательных числах объясняется, что число без знака считается положительным, поэтому плюс обычно не требуется.

Подробнее см. На нашей странице Дополнение .

— вычитание, минус, отрицательный

Этот символ имеет два основных применения в математике:

— используется, когда нужно вычесть одно или несколько чисел, например, 2 — 2.
Символ — также обычно используется для обозначения отрицательного или отрицательного числа, например −2.

См. Дополнительную информацию на нашей странице Вычитание .

× или * или. Умножение

Эти символы имеют то же значение; обычно × используется для обозначения умножения, когда написано от руки или используется на калькуляторе, например, 2 × 2.

Символ * используется в электронных таблицах и других компьютерных приложениях для обозначения умножения, хотя * имеет другие, более сложные значения в математике.

Реже умножение также может быть обозначено точкой. или вообще без символа. Например, если вы видите число, написанное вне скобок без оператора (символа или знака), то его следует умножить на содержимое скобок: 2 (3 + 2) то же самое, что 2 × (3 + 2).

См. Дополнительную информацию на нашей странице Умножение .

÷ или / Подразделение

Оба эти символа используются для обозначения деления в математике.÷ обычно используется в рукописных вычислениях и на калькуляторах, например, 2 ÷ 2.

/ используется в электронных таблицах и других компьютерных приложениях.

Подробнее см. На нашей странице Division .

= равно

Символ = равно используется, чтобы показать, что значения по обе стороны от него одинаковы. Чаще всего используется для отображения результата вычисления, например 2 + 2 = 4, или в уравнениях, например 2 + 3 = 10-5.

Вы также можете встретить другие похожие символы, но они встречаются реже:

≠ означает не равно. Например, 2 + 2 ≠ 5 — 2. В компьютерных приложениях (например, Excel) символы <> означают не равно.
≡ означает идентично. Это похоже на, но не совсем то же самое, что на равно. Поэтому, если сомневаетесь, придерживайтесь =.
≈ означает приблизительно равно или почти равно.Две стороны отношения, обозначенные этим символом, будут , а не достаточно точными для математических манипуляций.

<Меньше и> Больше

Этот символ < означает меньше, например 2 <4 означает, что 2 меньше 4.

Этот символ > означает больше, например, 4> 2.

≤ ≥ Эти символы означают «меньше или равно» и «больше или равно» и обычно используются в алгебре.В компьютерных приложениях используются <= и> =.

≪ ≫ Эти символы встречаются реже и означают намного меньше или намного больше.

± плюс или минус

Этот символ ± означает «плюс» или «минус». Он используется, например, для обозначения доверительных интервалов вокруг числа.

Ответом считается «плюс-минус» другое число, или, другими словами, в пределах диапазона данного ответа.

Например, 5 ± 2 на практике может быть любым числом от 3 до 7.

∑ Сумма

Символ ∑ означает сумму.

∑ — заглавная греческая буква сигма. Он обычно используется в алгебраических функциях, и вы также можете заметить его в Excel — кнопка Автосумма имеет сигму в качестве значка.

° Степень

Градусы ° используются по-разному.

В качестве меры поворота — угол между сторонами фигуры или поворот круга.Круг равен 360 °, а прямой угол — 90 °. См. Наш раздел о Геометрия для получения дополнительной информации.
Мера температуры. градусов по Цельсию или по Цельсию используются в большинстве стран мира (за исключением США). Вода замерзает при 0 ° C и закипает при 100 ° C. В США используется градус Фаренгейта. По шкале Фаренгейта вода замерзает при 32 ° F и закипает при 212 ° F. Смотрите нашу страницу: Системы измерения для получения дополнительной информации.

∠ Угол

Символ угла ∠ используется как сокращение в геометрии (изучении форм) для описания угла.

Выражение ∠ABC используется для описания угла в точке B (между точками A и C). Точно так же ∠BAC может использоваться для описания угла точки A (между точками B и C). Подробнее об углах и других геометрических терминах см. На наших страницах Геометрия .

√ Квадратный корень

√ — символ квадратного корня. Квадратный корень — это число, которое при умножении на себя дает исходное число.

Например, квадратный корень из 4 равен 2, потому что 2 x 2 = 4.Квадратный корень из 9 равен 3, потому что 3 x 3 = 9.

См. Нашу страницу: Специальные числа и понятия для получения дополнительной информации о квадратных корнях.

ⁿ Мощность

Целое число с верхним индексом (любое целое число n ) — это символ, используемый для обозначения степени числа.

Например, 3 ² означает 3 в степени 2, что совпадает с 3 в квадрате (3 x 3).

4 ³ означает 4 в степени 3 или 4 в кубе, то есть 4 × 4 × 4.

См. Наши страницы на Расчет площади и Расчет объема для примеров использования чисел в квадрате и кубе .

Степень также используется как сокращенный способ записи больших и малых чисел.

Большие числа

10 ⁶ — 1 000 000 (один миллион).

10 ⁹ — 1 000 000 000 (один миллиард).

10 ¹² — 1 000 000 000 000 (один триллион).6 = 10 ⁶ = 1000000 (один миллион).

. Десятичная точка

. — символ десятичной точки, часто называемый просто «точкой». См. Нашу страницу Decimals для примеров его использования.

, Разделитель тысяч

Запятую можно использовать для разделения больших чисел и облегчения их чтения.

Тысячу можно записать как 1000, так и 1000, а миллион — как 1000000 или 1000000.Запятая разделяет большие числа на блоки по три цифры.

В большинстве англоязычных стран, не имеет математической функции, он просто используется для облегчения чтения чисел.

В некоторых других странах, особенно в Европе, запятая может использоваться вместо десятичной точки, и, действительно, десятичная точка может использоваться вместо запятой в качестве визуального разделителя. Это объясняется более подробно на нашей странице Introduction to Numbers .

[], () Скобки, круглые скобки

Скобки () используются для определения порядка вычислений в соответствии с правилом BODMAS.

Части вычислений, заключенные в скобки, вычисляются первыми, например

5 + 3 × 2 = 11
(5 + 3) × 2 = 16

% В процентах

Символ% означает процент или число из 100.

Узнайте все о процентах на нашей странице: Введение в проценты

π Pi

π или пи — греческий символ звука «п».Это часто встречается в математике и является математической константой. Пи — это длина окружности, деленная на ее диаметр, и имеет значение 3,141592653. Это иррациональное число, что означает, что его десятичные разряды продолжаются до бесконечности.

∞ Бесконечность

Символ ∞ означает бесконечность — понятие, согласно которому числа существуют вечно.

Каким бы большим у вас ни было число, у вас всегда может быть номер побольше, потому что вы всегда можете добавить к нему еще один.

Бесконечность — это не число, а идея чисел, существующая вечно. Вы не можете прибавить единицу к бесконечности, как нельзя прибавить единицу к человеку, полюбить или ненавидеть.

\ (\ bar x \) (x-bar) Среднее значение

\ (\ bar x \) — среднее всех возможных значений x.

Чаще всего этот символ встречается в статистике.

См. Нашу страницу Средние значения для получения дополнительной информации.

! Факториал

! это символ факториала.

н! — произведение (умножение) всех чисел от n до 1 включительно, т.е. n × (n − 1) × (n − 2) ×… × 2 × 1.

Например:

5! = 5 × 4 × 3 × 2 × 1 = 120

10! = 10 × 9 × 8 × 7 × 6 × 5 × 4 × 3 × 2 × 1 = 3,628,800

| Труба

Труба ‘|’ также называется вертикальной чертой, vbar, pike и имеет множество применений в математике, физике и вычислениях.

Чаще всего в базовой математике он используется для обозначения абсолютного значения или модуля действительного числа, где \ (\ vert x \ vert \) — это абсолютное значение или модуль \ (x \) .

Математически это определяется как

$$ \ vert x \ vert = \ biggl \ {\ begin {eqnarray} -x, x \ lt 0 \\ x, x \ ge 0 \ end {eqnarray} $$

Проще говоря, \ (\ vert x \ vert \) — неотрицательное значение \ (x \). Например, модуль 6 равен 6, а модуль −6 также равен 6.

Он также используется в вероятности, где P (Z | Y) обозначает вероятность X с учетом Y.

∝ Пропорциональный

∝ означает «пропорционально » и используется, чтобы показать что-то, что изменяется по отношению к чему-то еще.

Например, если x = 2y, то x ∝ y.

∴ Следовательно

∴ — удобная сокращенная форма слова «поэтому», используемая в математике и естественных науках.

∵ Потому что

∵ — удобная сокращенная форма слова «потому что», не путать с «поэтому».

Математическая терминология (A-Z)

Амплитуда

Когда объект или точка движется циклически, или подвергается вибрации или колебаниям (например,грамм. маятник), амплитуда — это максимальное расстояние, на которое он перемещается от своей центральной точки. См. Введение в геометрию для получения дополнительной информации.

Апофема

Линия, соединяющая центр правильного многоугольника с одной из его сторон. Линия перпендикулярна (под прямым углом) в сторону.

Площадь

Геометрическая площадь определяется как пространство, занимаемое плоской формой или поверхностью объекта. Площадь измеряется в квадратных единицах, например в квадратных метрах (^{м 2}).Для получения дополнительной информации см. Нашу страницу, посвященную площади , площади поверхности и объему .

Асимптота

Асимптота — это прямая линия или ось, которая конкретно связана с изогнутой линией. По мере того, как кривая линия расширяется (стремится) к бесконечности, она приближается к своей асимптоте (то есть расстояние между кривой и асимптотой стремится к нулю, но никогда не касается ее). Встречается в геометрии и тригонометрии .

Ось

Опорная линия, вокруг которой нарисован, повернут или измерен объект, точка или линия.В симметричной форме ось обычно представляет собой линию симметрии.

Коэффициент

Коэффициент — это число или величина, умножающая другую величину. Обычно его ставят перед переменной . В выражении 6 x 6 — коэффициент, а x — переменная.

Окружность

Окружность — это длина расстояния по краю круга. Это тип с периметром , который уникален для круглых форм.Для получения дополнительной информации см. Нашу страницу, посвященную изогнутым формам .

Данные

Данные представляют собой набор значений, информации или характеристик, которые часто имеют числовой характер. Они могут быть собраны с помощью научного эксперимента или других средств наблюдения. Это могут быть количественных или качественных переменных. Датум — это одно значение одной переменной. См. Нашу страницу Типы данных для получения дополнительной информации.

Диаметр

Диаметр — это термин, используемый в геометрии для обозначения прямой линии, которая проходит через центр круга или сферы, касаясь окружности или поверхности с обоих концов.Диаметр в два раза больше радиуса .

Экстраполировать

Экстраполяция — это термин, используемый при анализе данных. Это относится к расширению графика, кривой или диапазона значений в диапазон, для которого нет данных, с выводом значений неизвестных данных из тенденций в известных данных.

Фактор

Коэффициент — это число, которое мы умножаем на другое число. Фактор делится на другое число целое число раз. У большинства чисел есть четное число факторов.Квадратное число имеет нечетное количество множителей. Простое число имеет два множителя — само себя и 1. Простой множитель — множитель, который является простым числом. Например, простые множители 21 равны 3 и 7 (потому что 3 × 7 = 21, а 3 и 7 — простые числа).

Среднее значение, медиана и мода

Среднее значение (среднее значение) набора данных вычисляется путем сложения всех чисел в наборе данных и последующего деления на количество значений в наборе.Когда набор данных упорядочен от наименьшего к наибольшему, медиана является средним значением. Режим — это число, которое встречается чаще всего.

Эксплуатация

Математическая операция — это шаг или этап в вычислении, или математическое «действие». Основные арифметические операции — это сложение, вычитание, умножение и деление. Порядок, в котором выполняются операции при вычислении, важен. Порядок действий известен как BODMAS .

Математические операции часто называют «суммами». Строго говоря, «сумма» — это операция сложения. В SYN мы имеем в виду операции и вычисления, но в повседневной речи вы часто можете услышать общий термин «суммы», который неверен.

Периметр

Периметр двумерной фигуры — это непрерывная линия (или длина линии), определяющая контур фигуры. Периметр круглой формы называется ее окружностью .Наша страница по периметру объясняет это более подробно.

Доля

Пропорция — это относительное отношение. Соотношения сравнивают одну часть с другой, а пропорции сравнивают одну часть с целым. Например, «3 из 10 взрослых в Англии имеют избыточный вес». Пропорция относится к дробям .

Пифагор

Пифагор был греческим философом, которому приписывают ряд важных математических и научных открытий, возможно, наиболее значительное из которых стало известно как Теорема Пифагора .

Это важное правило применяется только к прямоугольным треугольникам. В нем говорится, что «квадрат гипотенузы равен сумме квадратов на двух других сторонах».

Количественный и качественный

Количественные данные — это числовые переменные или значения, которые могут быть выражены численно, то есть сколько, сколько, как часто, и получаются путем подсчета или измерения.

Качественные данные — это переменные типа, которые не имеют числового значения и могут быть выражены описательно, т.е.е. с использованием имени или символа и получаются путем наблюдения.

Подробнее см. Нашу страницу о типах данных .

Радиан

Радиан — это единица измерения угла в системе СИ. Один радиан эквивалентен углу, образуемому в центре окружности дугой, равной по длине радиусу. Один радиан чуть меньше 57,3 градуса. Полный оборот (360 градусов) составляет 2π радиан.

Радиус

Термин радиус используется в контексте кругов и других изогнутых форм.Это расстояние от центральной точки круга, сферы или дуги до ее внешнего края, поверхности или окружности . Диаметр в два раза больше радиуса. Для получения дополнительной информации см. Нашу страницу, посвященную изогнутым формам .

Диапазон

В статистике диапазон данного набора данных — это разница между наибольшим и наименьшим значениями.

Коэффициент

Соотношение — это математический термин, используемый для сравнения размеров одной части с другой.Соотношения обычно отображаются в виде двух или более чисел, разделенных двоеточием, например, 7: 5, 1: 8 или 5: 2: 1.

Стандартное отклонение

Стандартное отклонение набора данных измеряет, насколько данные отличаются от среднего значения, то есть это мера вариации или разброса набора значений. Если разброс данных невелик и все значения близки к среднему, стандартное отклонение будет низким. Высокое стандартное отклонение указывает на то, что данные разбросаны по более широкому диапазону

Срок

Термин — это отдельное математическое выражение.Это может быть одно число, одна переменная (например, x ) или несколько констант и переменных, умноженных вместе (например, 3 x 2). Термины обычно разделяются операциями сложения или вычитания. Термин может включать операции сложения или вычитания, но только в скобках, например 3 (2 -x3).

Переменная

Переменная — это коэффициент в математическом выражении, арифметическом соотношении или научном эксперименте, которое может изменяться.В эксперименте обычно используются три типа переменных: независимые, зависимые и контролируемые. В выражении 6 x , 6 — это коэффициент , а x — переменная.

Разница

Дисперсия — это статистическое измерение, которое указывает разброс между элементами в наборе данных. Он измеряет, насколько далеко каждый член в наборе от среднего и, следовательно, от каждого другого члена в наборе.

Вектор

Векторы описывают математические величины, которые имеют как величину, так и направление.Векторы встречаются во многих математических и физических приложениях, например. изучение движения, где скорость, ускорение, сила, смещение и импульс являются векторными величинами.

Объем

Объем — это трехмерное пространство, занимаемое твердой или полой формой. Он измеряется кубическими размерами пространства, ограниченного его поверхностями. Объем измеряется в кубических единицах, например м ³.

Поперечное сечение подковы с геометрическими элементами и углами в трех точках…

Контекст 1

… 2 t — 1 ␪ = — arcsin ͑ 5 ͒ 4 2 t Когда t = 1 ͑ круговое поперечное сечение we, мы имеем ␪ = ␲ / 4 и центры для вершины дуга, нижняя дуга и две боковые дуги находятся в одном месте. Когда t = 3 и 2, мы имеем ␪ = ␲ / 4 — arcsin ͑ ͱ 2/3 ͒ = 0,294 515 или e = 0,129 17 r ͓ Eq. ͑ 3 ͔͒ для I-типа и ␪ = ␲ / 4 — arcsin ͑ ͱ 2/4 ͒ = 0,424 031 или e = 0,177 12 r для сечений II-типа соответственно. В таблице 1 приведены формулы для вычисления геометрических элементов ͑ смоченного периметра P и площади потока A ͒ в трех диапазонах глубины воды h ͒ для стандартного подковообразного поперечного сечения как функции углов ␣, ␤ и ␾, которые могут быть вычислены по заданной глубине. h ͑ Таблица 1 ͒.Lv et al. «2001» представила отдельные системы уравнений для расчета геометрических элементов для стандартных подковообразных сечений I-типа и II-типа. На рис.2 показаны безразмерная площадь A Ј = A / ͑ ␲ r 2 ͒, безразмерный гидравлический радиус R Ј h = R h / ͑ do / 4 ͒ и характеристический параметр AR 2 h / 3 / d 8 o / 3 как функция безразмерной глубины ͓ h / ͑ 2 r ͒ = h / do ͔ для стандартных подковообразных сечений I-типа и II, включая круглое сечение для сравнения ͑, где do = диаметр верхней дуги = 2 r r.На рис. 2 показано, что подковообразные поперечные сечения имеют большие площади потока и немного больший гидравлический радиус, чем круглое поперечное сечение на любой глубине воды. Безразмерный параметр AR 2 h / 3 / d 8 o / 3 равен nQ / ͓ ͱ S ͑ 2 r ͒ 8/3 ͔ на основании уравнения. ͑ 1 ͒ ͑ Уравнение Мэннинга ͒ и используется в качестве входного параметра в методе диаграммы для оценки нормальной глубины кругового канала ͑ Chow 1959 ͒. Поскольку геометрия подковообразного поперечного сечения сложна, как показано на рис.1, и задана в виде трех наборов сложных формул ͑ трансцендентных уравнений ͒ в таблице 1, прямого и аналитического решения нормальной глубины для подковообразных поперечных сечений с использованием Уравнение͑ 1 ͒. Можно использовать процедуру проб и ошибок, чтобы оценить нормальную глубину, используя уравнение. ͑ 1 ͒ и формулы в таблице 1, но это хлопотно и требует много времени с низкой точностью. Подставляя формулы для увлажненного периметра и площади в таблице 1 в уравнение. ͑ 1 ͒, мы разработали итерационные формулы для вычисления углов, соответствующих нормальной глубине в трех различных диапазонах глубин, и они сведены в Таблицу 2. После определения характеристических углов ␤, ␣ или using с использованием итерационных формул, можно использовать формулы в Таблица 1 для вычисления нормальной глубины hn.Начальные значения углов ␤ i и ␣ i устанавливаются как угол ␪ ͓ Eq. ͑ 5 ͔͒, а начальное значение ␾ i устанавливается как ␲ для запуска итерационного процесса. Обычно мы не знаем, к какому из трех случаев, представленных на рис. 1, относится нормальная глубина, когда нам нужно определить нормальную глубину для данного разряда. Поэтому мы вводим Q en как нормальный расход ͑ расход ͒, когда h n = e, и Q rn как нормальный расход, когда h n = r ͑ Lv et al. 2001. Q en и Q rn могут быть вычислены с использованием следующих формул, представленных в виде Ур.͑ 6 ͒ и ͑ 7 ͒. Для стандартного поперечного сечения I-образной подковы ͑ t = 3 …

Context 2

… 2 t — 1 ␪ = — arcsin ͑ 5 ͒ 4 2 t При t = 1 ͑ круглое поперечное сечение ͒ , мы имеем ␪ = ␲ / 4 и центры верхней дуги, нижней дуги и двух боковых дуг находятся в одном месте. Когда t = 3 и 2, мы имеем ␪ = ␲ / 4 — arcsin ͑ ͱ 2/3 ͒ = 0,294 515 или e = 0,129 17 r ͓ Eq. ͑ 3 ͔͒ для I-типа и ␪ = ␲ / 4 — arcsin ͑ ͱ 2/4 ͒ = 0,424 031 или e = 0,177 12 r для сечений II-типа соответственно.В таблице 1 приведены формулы для вычисления геометрических элементов ͑ смоченного периметра P и площади потока A ͒ в трех диапазонах глубины воды h ͒ для стандартного подковообразного поперечного сечения как функции углов ␣, ␤ и ␾, которые могут быть вычислены по заданной глубине. h ͑ Таблица 1 ͒. Lv et al. «2001» представила отдельные системы уравнений для расчета геометрических элементов для стандартных подковообразных сечений I-типа и II-типа. На рис.2 показаны безразмерная площадь A Ј = A / ͑ ␲ r 2 ͒, безразмерный гидравлический радиус R Ј h = R h / ͑ do / 4 ͒ и характеристический параметр AR 2 h / 3 / d 8 o / 3 как функция безразмерной глубины ͓ h / ͑ 2 r ͒ = h / do ͔ для стандартных подковообразных сечений I-типа и II, включая круглое сечение для сравнения ͑, где do = диаметр верхней дуги = 2 r r.На рис. 2 показано, что подковообразные поперечные сечения имеют большие площади потока и немного больший гидравлический радиус, чем круглое поперечное сечение на любой глубине воды. Безразмерный параметр AR 2 h / 3 / d 8 o / 3 равен nQ / ͓ ͱ S ͑ 2 r ͒ 8/3 ͔ на основании уравнения. ͑ 1 ͒ ͑ Уравнение Мэннинга ͒ и используется в качестве входного параметра в методе диаграммы для оценки нормальной глубины кругового канала ͑ Chow 1959 ͒. Поскольку геометрия подковообразного поперечного сечения сложна, как показано на рис.1, и задана в виде трех наборов сложных формул ͑ трансцендентных уравнений ͒ в таблице 1, прямого и аналитического решения нормальной глубины для подковообразных поперечных сечений с использованием Уравнение͑ 1 ͒. Можно использовать процедуру проб и ошибок, чтобы оценить нормальную глубину, используя уравнение. ͑ 1 ͒ и формулы в таблице 1, но это хлопотно и требует много времени с низкой точностью. Подставляя формулы для увлажненного периметра и площади в таблице 1 в уравнение. ͑ 1 ͒, мы разработали итерационные формулы для вычисления углов, соответствующих нормальной глубине в трех различных диапазонах глубин, и они сведены в Таблицу 2. После определения характеристических углов ␤, ␣ или using с использованием итерационных формул, можно использовать формулы в Таблица 1 для вычисления нормальной глубины hn.Начальные значения углов ␤ i и ␣ i устанавливаются как угол ␪ ͓ Eq. ͑ 5 ͔͒, а начальное значение ␾ i устанавливается как ␲ для запуска итерационного процесса. Обычно мы не знаем, к какому из трех случаев, представленных на рис. 1, относится нормальная глубина, когда нам нужно определить нормальную глубину для данного разряда. Поэтому мы вводим Q en как нормальный расход ͑ расход ͒, когда h n = e, и Q rn как нормальный расход, когда h n = r ͑ Lv et al. 2001. Q en и Q rn могут быть вычислены с использованием следующих формул, представленных в виде Ур.͑ 6 ͒ и ͑ 7 ͒. Для стандартного поперечного сечения подковы I-типа ͑ t = 3 …

Контекст 3

… Q = расход ͑ м / с ͒, заданный для вычисления соответствующей нормальной глубины; n = коэффициент шероховатости Маннинга в зависимости от материалов футерованного канала ͑ Chow 1959 ͒; A = площадь поперечного сечения потока ͑ м 2 ͒; R h = гидравлический радиус ͑ м ͒ = A / P; P = смоченный периметр ͑ м ͒; и S = наклон русла канала или наклон энергии при нормальном или равномерном потоке. Не существует аналитического решения для прямого расчета нормальной глубины в любых поперечных сечениях открытого канала, кроме треугольных каналов ͑ Chow 1959.Wang et al. ͑ 1998 разработала формулу оценки для прямого расчета нормальной глубины в трапециевидном канале с относительной погрешностью менее 1,8%. Zhao et al. ͑ 2008 ͒ и Zhang et al. ͑ 2009 ͒ разработаны формулы для расчета нормальной глубины кольцевых каналов. Wang et al. ͑ 1999 ͒ и Babaeyan-Koopaei ͑ 2001 разработали формулы или кривые для расчета нормальных глубин секций русла со сферическим или параболическим дном. Swamee ͑ 1994 разработал уравнение равномерного потока как функцию высоты шероховатости поверхности канала и кинематической вязкости жидкости, и, используя аппроксимацию кривой, он получил неявные уравнения, вычисляющие нормальные глубины в треугольных, широких прямоугольных и узких прямоугольных сечениях.Swamee и Rathie ͑ 2004 of получили точное решение нормальных глубин в терминах бесконечного ряда для различных участков открытого канала. Многие проектировщики и инженеры по-прежнему обычно используют метод диаграммы Chow 1959 для трапециевидных и круговых каналов или итеративную процедуру или процедуру проб и ошибок для других сложных каналов с различной степенью погрешности при вычислении нормальной глубины. Подковообразное поперечное сечение является одним из часто используемых поперечных сечений для туннелей транспортировки воды со свободной поверхностью из-за превосходных структурных и гидравлических характеристик ͑ Chengdu University of Science and Technology 1979 ͒.Стандартные поперечные сечения подковы использовались в Турции в течение последних 4000 лет ͑ Ozis 1996 ͒ и были спроектированы и построены Бюро мелиорации США Hu 1973 ͒ и для многих гидравлических проектов в Китае ͑ Lv et al. 2001 ͒ и несколько других стран ͑ Merkley 2005. Поскольку геометрия поперечного сечения подковы сложна, невозможно получить аналитическое решение нормальной глубины из уравнения. ͑ 1 ͒. Lv et al. ͑ 2001 ͒ разработал итерационный метод расчета нормальной глубины для поперечного сечения подковы.Однако их формулы не являются общими для всех типов подковообразных сечений. На сегодняшний день не существует общих расчетных формул для расчета нормальной глубины туннелей с подковообразным поперечным сечением. В этой заметке представлены итерационные формулы для расчета нормальной глубины, которые могут применяться для всех типов подковообразных поперечных сечений. На основе принципа постепенной подгонки оптимизации ͑ Zheng and Liu 2001 были разработаны общие формулы оценки, дающие прямое решение нормальной глубины стандартных подковообразных поперечных сечений.Для проверки точности формул были проанализированы относительные погрешности нормальных глубин стандартных подковообразных сечений I-типа и II-типа. Поперечное сечение подковы состоит из четырех сегментов дуги: верхней дуги с радиусом r m ͒, двух боковых дуг и нижней дуги с тем же радиусом R ͑ m, но с разными центрами окружности ͑ Рис. 1. Ху (1973) и Меркли (2005) представили сложные уравнения для вычисления геометрии стандартного поперечного сечения подковы II типа. Для общего сечения подковы определяется характерный параметр t…

Контекст 4

… t = 1 или R = r, поперечное сечение подковы точно такое же, как круглое поперечное сечение. Когда t = 3 или R = 3 r, оно называется стандартным поперечным сечением подковы I типа, а когда t = 2 или R = 2 r, оно называется стандартным поперечным сечением подковы II типа ͑ Lv et al. 2001. На рис. 1 показано общее сечение подковы и соответствующие геометрические элементы и углы на трех разных глубинах воды h ͒: ͑ 1 ͒ 0 Յ h Յ e; ͑ 2 ͒ е Յ ч Յ р; и ͑ 3 ͒ r Յ h Յ 2 r.e — высота нижней дуги ͑ Рис. 1 ͒ и может быть вычислена …

Контекст 5

… t = 1 или R = r, поперечное сечение подковы точно такое же, как у окружности поперечное сечение. Когда t = 3 или R = 3 r, оно называется стандартным поперечным сечением подковы I типа, а когда t = 2 или R = 2 r, оно называется стандартным поперечным сечением подковы II типа ͑ Lv et al. 2001. На рис. 1 показано общее сечение подковы и соответствующие геометрические элементы и углы на трех разных глубинах воды h ͒: ͑ 1 ͒ 0 Յ h Յ e; ͑ 2 ͒ е Յ ч Յ р; и ͑ 3 ͒ r Յ h Յ 2 r.e — высота нижней дуги ͑ Рис. 1 ͒ и может быть вычислена …

The Horse Horseshoe Boots Вирусная головоломка — правильный ответ объяснен — помните о своих решениях

Многие люди спорят о правильном ответе на этот проблема, которая уже имеет более 500 000 комментариев в Facebook.

Сможете разобраться? Посмотрите видео, чтобы узнать о решении.

The Horse Horseshoe Boots Вирусная алгебра Задача — правильный ответ объяснен

Или продолжайте читать, чтобы найти ответ.
.
.

«Все будет хорошо, если ты будешь использовать свой разум для принятия решений, и думать только о своих решениях». С 2007 года я посвятил свою жизнь разделению радости теории игр и математики. MindYourDecisions теперь имеет более 1000 бесплатных статей без рекламы благодаря поддержке сообщества! Помогите и получите ранний доступ к сообщениям с обещанием на Patreon.

.
.

.
.
.
.
M
I
N
D
.
Y
O
U
R
.
D
E
C
I
S
I
O
N
S
.
.
.
.
Answer To The Horse Horseshoe Boots Вирусная головоломка

Одна сложная часть проблемы заключается в том, что третье уравнение имеет 2 подковы и 2 ботинка, а в четвертой строке только 1 подкова и 1 ботинок.

Теперь давайте решим стоимость каждого предмета. Из первого уравнения мы можем решить, что лошадь равна 10.

Из второго мы можем решить, что каждая подкова равна 2.

Затем из третьего мы можем решить, что ценность ботинка равна равно 1.

Затем нам нужно оценить значение плюс ботинка (лошадь × подкова). Это 1 + 10 × 2 = 1 + 20 = 21.

(10 × 2 оценивается первым по порядку операций, потому что умножение имеет приоритет над сложением).

Следовательно, правильный ответ — 21.

Эта задача похожа на задачу алгебры цветов и задачу алгебры фруктов, которые также стали вирусными и вызвали много дискуссий.

Источники
Сообщение в Facebook
https: // www.facebook.com/photo.php?fbid=10205775670504946&set=a.3886338930910.126365.1652018492&type=3

The Telegraph
http://www.telegraph.co.uk/news/2016/09/05/this-simple-algebra- question-is-confusing-the-internet-can-you /

Опубликовано

PRESH TALWALKAR

Я веду канал MindYourDecisions на YouTube, у которого более 1 миллиона подписчиков и 200 миллионов просмотров. Я также являюсь автором книги «Радость теории игр: введение в стратегическое мышление» и нескольких других книг, доступных на Amazon.

(Как и следовало ожидать, ссылки на мои книги ведут в их списки на Amazon. Как партнер Amazon я зарабатываю на соответствующих покупках. Это не влияет на цену, которую вы платите.)

Из истории я начал Блог Mind Your Decisions в 2007 году, в котором рассказывается немного о математике, личных финансах, личных мыслях и теории игр. Это было настоящее путешествие! Я благодарю всех, кто поделился моей работой, и я очень благодарен за освещение в прессе, включая Shorty Awards, The Telegraph, Freakonomics и многие другие популярные издания.

Я изучал экономику и математику в Стэнфордском университете.

Люди часто спрашивают, как я снимаю видео. Как и многие ютуберы, я использую популярное программное обеспечение для подготовки своих видео. Вы можете найти на YouTube учебники по программному обеспечению для анимации, чтобы узнать, как снимать видео. Будьте готовы — анимация отнимает много времени, а программное обеспечение может быть дорогим!

Не стесняйтесь, пришлите мне электронное письмо [электронная почта защищена]. Я получаю так много писем, что могу не отвечать, но я сохраняю все предложения для головоломок / тем для видео.

МОИ КНИГИ

Если вы совершаете покупки по этим ссылкам, я могу получить компенсацию за покупки, сделанные на Amazon. Как партнер Amazon я зарабатываю на соответствующих покупках. Это не влияет на цену, которую вы платите.

(ссылки для США и других стран)
https://mindyourdecisions.com/blog/my-books

Mind Your Decisions — это сборник из 5 книг:

(1) The Joy of Game Theory: An Introduction to Strategic Мышление
(2) 40 парадоксов в теории логики, вероятностей и игр
(3) Иллюзия иррациональности: как принимать разумные решения и преодолевать предвзятость
(4) Лучшие уловки в области умственной математики
(5) Умножать числа, рисуя линии

The Joy of Game Theory показывает, как можно использовать математику, чтобы перехитрить своих конкурентов.(рейтинг 4,2 / 5 звезд в 184 отзывах)

40 Парадоксов в теории логики, вероятностей и игр содержит наводящие на размышления и противоречащие интуиции результаты. (рейтинг 4/5 звезд в 28 обзорах)

Иллюзия иррациональности: как принимать разумные решения и преодолевать предвзятость — это руководство, в котором объясняется, насколько мы необъективны при принятии решений, и предлагаются методы для принятия разумных решений. (рейтинг 3,9 / 5 звезд в 16 отзывах)

Лучшие уловки в области ментальной математики учит, как можно выглядеть гением математики, решая задачи в уме (оценка 4.2/5 звезд в 52 обзорах)

Умножение чисел на рисованные линии Эта книга представляет собой справочное руководство для моего видео, которое набрало более 1 миллиона просмотров о геометрическом методе умножения чисел. (рейтинг 4,1 / 5 звезд в 22 обзорах)

Mind Your Puzzles — это сборник из трех книг «Математические головоломки», тома 1, 2 и 3. Темы головоломок включают математические предметы, включая геометрию, вероятность и т. д. логика и теория игр.

Math Puzzles Volume 1 содержит классические головоломки и загадки с полными решениями задач счета, геометрии, вероятности и теории игр.Том 1 получил оценку 4,4 / 5 звезд в 66 отзывах.

Math Puzzles Volume 2 — это продолжение книги с более серьезными задачами. (рейтинг 4,2 / 5 звезд по 19 отзывам)

Math Puzzles Volume 3 — третий в серии. (рейтинг 4,2 / 5 звезд по 15 отзывам)

KINDLE UNLIMITED

Учителя и студенты со всего мира часто пишут мне о книгах. Поскольку образование может иметь такое огромное влияние, я стараюсь сделать электронные книги доступными как можно шире по как можно более низкой цене.

В настоящее время вы можете читать большинство моих электронных книг с помощью программы Amazon Kindle Unlimited. Включив подписку, вы получите доступ к миллионам электронных книг. Вам не нужно устройство Kindle: вы можете установить приложение Kindle на любой смартфон / планшет / компьютер и т. Д. Ниже я собрал ссылки на программы в некоторых странах. Пожалуйста, проверьте доступность и условия программы на своем местном веб-сайте Amazon.

США, список моих книг (США)
Великобритания, список моих книг (Великобритания)
Канада, результаты книги (CA)
Германия, список моих книг (DE)
Франция, список моих книг (FR)
Индия , список моих книг (IN)
Австралия, результаты книг (AU)
Италия, список моих книг (IT)
Испания, список моих книг (ES)
Япония, список моих книг (JP)
Бразилия, книга results (BR)
Мексика, книга результатов (MX)

MERCHANDISE

Купите кружку, футболку и многое другое на официальном сайте товаров: Mind Your Decisions at Teespring .

Подкова Смейла — Scholarpedia

Рисунок 1: Подкова Смейла. (Это изображение было создано Биллом Кассельманом, графическим редактором Уведомлений Американского математического общества. Впервые оно появилось в статье М. Шуба в выпуске Уведомлений Американского математического общества за май 2005 г.)

Подкова Смейла — визитная карточка хаоса. С поразительным геометрическая и аналитическая ясность, он надежно описывает гомоклиническую динамика, встреченная Пуанкаре и изученная Биркгофом, Картрайт-Литтлвуд и Левинсон.Сначала приведем пример и определения позже.

Рассмотрим вложение \ (f \) диска \ (\ Delta \) в себя. выставлен на рисунке. Он стягивает полудиски \ (A \, \) \ (E \) к полудиски \ (f (A) \, \) \ (f (E) \) в \ (A \; \) и посылает прямоугольники \ (B \, \) \ (D \) линейно к прямоугольникам \ (f (B) \, \) \ (f (D) \, \), растягивая их вертикально и сжимая их по горизонтали. В случае \ (D \, \) это также поворачивается на 180 градусов. Нам все равно, что за изображение \ (f (C) \) из \ (C \) до тех пор, пока он не пересекает прямоугольник \ (B \ cup C \ cup D \.п (г) \ rightarrow p \] как \ (n \ rightarrow — \ infty \} \) стабильны и нестабильны многообразия \ (p \. T \) имеет также подкова, содержащая \ (r \, \) и, следовательно, имеющая хаос сдвига.В наши дни этот факт нетрудно увидеть даже в более высоких измерениях. Само существование поперечного пересечения между стойлами а из неустойчивых многообразий периодической орбиты следует подкова. В случае потоков соответствующее утверждение верно для Карта Пуанкаре. Резюмируя,

поперечная гомоклиничность \ (\ Rightarrow \) подкова \ (\ Rightarrow \) хаос.

Поскольку трансверсальность сохраняется при возмущении следует то же самое делает подкова, и так же хаос.

Аналитическая характеристика подковы — гиперболичность — явление сжатия / растяжения, выраженное через производную. Производная от \ (f \) растягивает касательные векторы, параллельные к вертикали и сжимает векторы параллельно горизонтали, не только в седловых точках, но и равномерно по всей \ (\ Lambda \. \) В общем случае гиперболичность компактного инвариантного множества, такого как \ (\ Lambda \) в любом измерении выражается в терминах расширения и сжатие производной на подрасслоениях касательной пучок.Смейл объединил такие примеры, как подкова и геодезический поток на многообразиях отрицательной кривизны, определяющий, что теперь называемые равномерно гиперболическими динамическими системами. Это системы, в которых неблуждающее множество является равномерно гиперболическим множеством, и его устойчивые и неустойчивые многообразия трансверсальны во всех точках или, по крайней мере, не имеют циклов (см., например, книгу Шуба ниже для точных определений). Изучение эти системы привели ко многим плодотворным открытиям в современной теория динамических систем.

Дэвид Рюэлль имеет назвал статью Смейла 1967 года «шедевр математической литература. «Это все еще стоит прочитать сегодня. Гиперболическая динамика процветала в 1960-х и 1970-х годах. Аносов доказали структурную устойчивость и эргодичность глобального гиперболические системы, которые сейчас носить его имя. Синай положил начало более общее расследование эргодическая теория гиперболических динамические системы, а в в частности показал, что Марковские перегородки Адлера и Вайса могли быть построены для всех гиперболических инвариантные множества, таким образом давая кодирование аналогично двухсменному кодирование для подковы.Эта работа был перенесен Руэлем и Боуэн. Инвариантные меры они обнаружили, что теперь называемые мерами Синая-Рюэля-Боуэна (SRB-меры), описывают асимптотические динамика самого Лебега точек на многообразии даже при диссипативные системы. Равномерно гиперболический динамические системы замечательный. Они демонстрируют хаотичное поведение. Посредством работы Аносова, Смейла, Палиса и Роббин они структурно стабильное или неблуждающее множество стабильное, то есть динамика возмущение равномерно гиперболическая система топологически сопряжены с оригинал глобально или, по крайней мере, ограничен неблуждающими множествами.По работы Синая, Рюэля, Боуэна они описаны статистически.

В начале 60-х гг. надеялись, что единообразно гиперболический динамические системы могут быть в какой-то смысл типичный. В то время как они сформировать большой открытый набор на всех многообразия они не плотны. Поиск типичные динамические системы продолжает оставаться большой проблемой. Для прогресса см. обзор Bonatti et al. (2004). Гиперболические периодические точки, их глобальная стабильность и нестабильность многообразия и гомоклинические точки остаются одними из главных особенности и инструменты для понимание динамики хаотичный системы.

Действительно поперечная гомоклиника доказано, что точки существуют во многих динамических систем встречается в науке и инженерное дело из небесной механики, где Пуанкаре впервые заметил их к экология и не только.

История

История открытия подковы и состояния математики в 1960 году подробно описана Смейлом (1998).

Подкова — естественное следствие геометрического взгляда на уравнения Картрайта-Литтлвуда и Левинсона.Это помогает понять механизм хаоса и объяснить широко распространенную непредсказуемость динамики. Он был открыт в 1960 году в Рио-де-Жанейро, когда доктор Смейл получал поддержку от Национального научного фонда США в качестве постдокторанта. Доктор Смейл был принят в Instituto da Matematica, Pura e Aplicada (IMPA), финансируемом правительством Бразилии, что обеспечило приятные офисные и рабочие условия. (Впоследствии были подняты вопросы о том, что он использовал U.Деньги налогоплательщика С. на исследования, проведенные на пляжах Рио. Фактически никто иной, как научный советник президента Джонсона Дональд Хорниг, писал по этому поводу в 1968 году в широко распространяемом журнале Science.)

В Рио Смейл проводил исследования в области математики, которая должна была стать теорией хаоса. В то время как тополог он гордился только что опубликованной им работой по динамике. Он был в восторге от гипотезы в этой статье, которая, как следствие (в современной терминологии), «хаоса не существует»! Эту эйфорию вскоре разрушило письмо, полученное от М.ЭТО. математик по имени Норман Левинсон. Он был соавтором основного дипломного текста по обыкновенным дифференциальным уравнениям и был ученым, которого следовало воспринимать всерьез. Левинсон описал свой более ранний результат, который фактически содержал контрпример к гипотезе Смейла. Статья Левинсона, в свою очередь, была разъяснением обширной работы пары британских математиков Мэри Картрайт и Дж. Л. Литтлвуда, проделанной во время Второй мировой войны. Картрайт и Литтлвуд занимался анализом некоторых уравнений, возникающих при проведении связанных с войной исследований с использованием радиоволн.Они обнаружили неожиданное и необычное поведение решений этих уравнений. Фактически Картрайт и Литтлвуд математически доказали, что признаки хаоса могут существовать даже в уравнениях, естественным образом возникающих в инженерии. Но мир не был готов слушать, и даже сегодня их важный вклад в теорию хаоса малоизвестен. Чтобы понять контрпример Левинсона, необходимо было перевести его аналитические аргументы в геометрический образ мышления, что привело к открытию подковы.

Список литературы

Бонатти, Лоренцо Дж. Диас, Марсело Виана, Динамика за пределами однородной гиперболичности: глобальный геометрический и вероятностный подход, Энциклопедия математических наук , Springer, 2004.

Майкл Шуб, Глобальная стабильность динамических систем , Спрингер, 1986.

Майкл Шуб, Что такое подкова? , Уведомления AMS, v.52, p.530-532

Стивен Смейл, Дифференцируемые динамические системы, Бюлл.Амер. Математика. Soc.73 (1967), 747-817.

Стив Смейл, В поисках подковы на пляжах Рио, Mathematical Intelligencer 20 (1998), 39-44.

Внутренние ссылки

См. Также

Хаос, эргодическая теория, гомоклинические орбиты, гиперболическая динамика, итерационные отображения, бифуркация Шильникова, мера SRB, структурная устойчивость, символьная динамика [Категория: Несколько кураторов]]

Карта подковы Смейла с помощью троичных чисел в JSTOR

Abstract

Подковообразное отображение Смейла стало стандартным примером при изучении дискретных динамических систем.Подковообразное отображение Смейла встречается в широком круге физических задач с хаотической динамикой на инвариантном множестве. Его хаотическое поведение обычно показывают, сначала сопоставляя его с картой двустороннего сдвига. Авторы дают более элементарную трактовку частного, но типичного случая. Единственная необходимая техническая подготовка — это множество Кантора и его троичное представление.

Информация о журнале

SIAM Review содержит статьи, написанные для широкого круга читателей. научная аудитория.Статьи включают пояснительные или обзорные статьи. сосредоточение внимания на важных достижениях в прикладной или вычислительной математике, или документы, описывающие математические и вычислительные задачи в научные или инженерные приложения. Другие функции включают эссе, обзоры книг, тематические исследования из отрасли, классные заметки и проблемы и решения.

Информация об издателе

«Общество промышленной и прикладной математики является ведущим международная ассоциация прикладной математики и ее публикации мог бы стать ядром адекватного собрания по математике.

что значит в геометрии подкова в бок «с»

Что означает символ подковы? Значение подковы на стенах дома и крышках гроба

Что означает?

КАК ОПРЕДЕЛИТЬ РАЗМЕР КОЛЬЦА? | www.zolpodkova.ru

«Народные поверья. Оберег своими руками – «Подкова – символ счастья»

Подкова, торговая сеть отзывы и оценка

Форма подкова с пожеланиями на 62гр (мд) пластик

Причины биения и вибрации автомобиля.

Виды вибрации и биения

Неисправности

Хаотическая подкова Смейла | plus.maths.org

Подкова

Подкова динамика

Переменная динамика

Об этой статье

Введение в математические символы для соединения и пересечения

Теория множеств для объединения и пересечения

Компьютеры для программирования с помощью «И» и «ИЛИ»

Сводка математических символов для пересечения и объединения, и и или

Общие математические символы и терминология

Общие математические символы

+ сложение, плюс, положительное

— вычитание, минус, отрицательный

× или * или. Умножение

÷ или / Подразделение

= равно

± плюс или минус

∑ Сумма

° Степень

∠ Угол

√ Квадратный корень

. Десятичная точка

, Разделитель тысяч

[], () Скобки, круглые скобки

% В процентах

π Pi

∞ Бесконечность

\ (\ bar x \) (x-bar) Среднее значение

! Факториал

| Труба

∝ Пропорциональный

∴ Следовательно

∵ Потому что

Математическая терминология (A-Z)

Поперечное сечение подковы с геометрическими элементами и углами в трех точках…

The Horse Horseshoe Boots Вирусная головоломка — правильный ответ объяснен — ​​помните о своих решениях

Опубликовано

PRESH TALWALKAR

МОИ КНИГИ

KINDLE UNLIMITED

MERCHANDISE

Подкова Смейла — Scholarpedia

История

Список литературы

См. Также

Карта подковы Смейла с помощью троичных чисел в JSTOR

Добавить комментарий Отменить ответ

The Horse Horseshoe Boots Вирусная головоломка — правильный ответ объяснен — помните о своих решениях